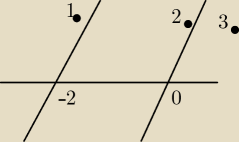
Nierówność kwadratowa z wartością bezwzględną TheLawPL: Pani od matmy wymyśliła taką nierówność: 6x²+15|x+2|−20|x|−17x−18≥0 x=−2 x=0 Rysunek powyżej 1. (−∞;−2> Skąd potem wzięło się takie coś: 6²−15x−30+20x−17x−18≥0 I jeszcze jedno pytanko: Jak po zrobieniu punktów takiej nierównośći napisać odpowiedź, tzn. wskazać wspólną część?

PW: Ten rysunek pokazuje przebieg funkcji g(x)=|x+2| i h(x)=|x|. Jednym z możliwych do rozpatrzenia przedziałów jest (−∞,−2), na którym obie te funkcje przyjmują wartości ujemne. Skoro tak, to g(x)=−x−2 i h(x)=−x, dlatego nierówność 6x²+15(−x−2)−20(−x)−17x−18≥0 6x²−15x−30+20x−17x−18≥0, x∊ (−∞,−2). Rozwiązać do końca zwracając uwagę na dziedzinę. Ale to jest dopiero 1/3 zadania (jeszcze na przedziałach <−2,0) <0,∞).