Proszę o pomoc i dokończenie Marysia: 1. Wykonaj wskazane działanie:

3		4
	−		=
2x−1		x+2

Marysia: wiem, że będzie teraz 3(x+2)−4(2x−1) przez (2x−1)(x+2) trzeba teraz pomnożyć, czyli 3x+6−8x−4 przez (2x−1)(x+2) Nie wiem jak to się robi. Może ktoś mi pomóc?

Kaja:

3(x+2)		4(2x−1)		3x+6		8x−4
	−		=		−		=
(2x−1)(x+2)		(2x−1)(x+2)		(2x−1)(x+2)		(2x−1)(x+2)

	−5x+10
=
	(2x−1)(x+2)

krzysiek: sprowadź do wspólnego mianownika a później już możesz odejmować

Marysia: aa to Ty jeszcze inaczej zrobiłaś. Dziękuje bardzo

bezendu: Ale najpierw zanim zaczniesz cokolwiek robić wyznacz dziedzinę

Marysia: 1. Oblicz sumę n początkowych wyrazów ciągu arytmetycznego, jeżeli a₁ = 100 , r = −2 , n = 50 2. Wykonaj wskazane działanie:

2		3
	+		=
a−1		2a+1

Marysia: jak dziedzinę?

Kaja: 1. a₅₀=100+49*(−2)=2

Marysia: Pomożecie też w tych zadaniach?

Marysia: i to jest całe zadanie 1?

Kaja: zał. 2x−1≠0 i x+2≠0 x≠0,5 i x≠−2 D=R/{−2;0,5}

Kaja: tak całe

Kaja: oj przepraszam nie całe. zaraz dokończę

Marysia: wydawało się trudne i dłuższe przede wszystkim

bezendu: 1. a₅₀=100+(50−1)*(−2) a₅₀=100−98 a₅₀=2

	100+2
S50=		*50=2550
	2

2) chyba już potrafisz sama zrobić

Kaja:

	a1+a50
ad. 1. S50=		*50=2550
	2

Marysia: No właśnie też tak patrzyłam Nic się nie stało W ogóle bardzo dziękuje za pomoc. Mogę liczyć na dalszą? Troszkę tych zadań mam do zrobienia, a nie zrobię tego sama

Marysia: tak potrafię, Dzięki bezendu

Kaja: w zad. 2 sprowadź sobie do wspólnego mianownika (zrób podobnie jak to z tym odejmowaniem)

bezendu: to pokaż jak liczysz poprawimy ewentualnie

Marysia: 1. Oblicz sumę liczb naturalnych od 1 do 50. 2. Rozwiąż nierówność:

2x−5
	≤3
x−3

Marysia: czyli wspólny mianownik to będzie: (a−1)(2a+1)?

bezendu: 1. a₁=1 a_n=50 n=50

	1+50
S50=		*50=1275
	2

2.Sama spróbuj

Marysia: Pomóżcie.. plisss

bezendu: 2(2a+1)+3(a−1)=0 dokończ

Marysia: Nie porafię zrobić sama, nie będę ukrywać, że matma to nie dla mnie. Nic nie wydukam

Marysia: mam się pozbyć nawiasów teraz? Czyli: 4a+2+3a−3=0?

bezendu: https://matematykaszkolna.pl/strona/1696.html Marysia coś kręcisz ;> bierzesz się za nierówności wymierne które są na rozszerzeniu a podstaw nie znasz poczytaj to co masz w linku

bezendu: w równaniu wymiernym interesuje Cię licznik i dziedzina tylko

Marysia: Wiesz nie umiem w ogóle matmy. Korki też mi nie pomogły. Mogę przeczytać tylko w tej chwili nic mi to nie da W tym problem

Kaja:

2*(2a+1)+3(a−1)		4a+2+3a−3		7a−1
	=		=
(2a+1)(a−1)		(2a+1)(a−1)		(2a+1)(a−1)

zał. 2a+1≠0 i a≠1 a≠−0,5 po prostu mianowniki nie mogą być zerami bo przez zero nie wolno dzielić

bezendu: 4a+2+3a−3=0 7a−1=0 7a=1 /7

	1
a=		∊D
	7

	1
więc rozwiązaniem równania jest x=		i to tyle w tym temacie
	7

Marysia:

Marysia: Dla was to proste, dla mnie niestety Masakra

Marysia: Nie mogę się teraz połapać przykłady do jakich zadań teraz są

bezendu:

2x−5
	≤3
x−3

	5
Df=ℛ\{3;		}
	2

2x−5
	−3≤0
x−3

2x−5		3(x−3)
	−		≤0
x−3		x−3

2x−5−3x+9
	≤0
x−3

−x+4
	≤0
x−3

(−x+4)(x−3)≤0 dokończ

Kaja: popatrz sobie na mój post z godziny 12:06. tam masz rozwiązane zadanie to z literką a.

Marysia:

	2x−5
A ten przykład : Rozwiąż nierówność		≤3
	x−3

bezendu: a ten przykład masz dokończyć sama, masz rozpisany w poście 12:13

Marysia: jak ja mam to dokończyć? Nie łapie sie w tym, sorry

Kaja: zad. oblicz sumę liczb naturalnych od 1 do 50: a₁=1 a₅₀=50 n=50 r=1

	1+50
S50=		*50=1275
	2

bezendu: to popatrz link... po to Ci go wysłałem, Ty wgl nic nie próbujesz zrobić sama...

bezendu: @Kaja to zadanie już zrobiłem 11:58 nie potrzebne to jest r

Kaja: wiem, że nie potrzebne, ale nie zaszkodzi napisać

Marysia: no czytałam ten link co mi wysłałeś

bezendu: a popatrz jeszcze na mój post z godz 12:13 czy się nigdzie nie pomyliłem

bezendu: @Marysia jak przejrzałaś ten link to teraz wiesz jak to dokończyć czekam na Twoją odpowiedź

Marysia: A tak jest?

Marysia: powiem Ci tak, że na tym linku nic nie ma takieo co by podpowiedziało mi jak dokończyć to zadanie

Marysia: nie dla mnie

Kaja:

	5
bezendu odnośnie tego postu z 12:13 , tam nie trzeba z dziedziny wyrzucać		. dziedzina to
	2

D=R/{3}

bezendu: to widocznie go nie przeglądałaś zobacz inne rozwiązania jeszcze

bezendu: @Kaja dziękuję

Kaja: proszę

Marysia:

Marysia:

	7a4b		8xy5
1. Wykonaj wskazane działanie:		*		=
	4x2y		21a3b2

Marysia: nie wiem jak to dokończyć. Pomożesz w tamtym zadaniu? Nie wiem w ogóle o co chodzi?

Kaja: Marysia chwilkę jeszcze tamto zadanie co bezendu nie dokończył. (−x+4)(x−3)≤0 miejsca zerowe tej lewej strony nierówności to 4 i 3. parabola będąca wykresem lewej strony nierówności powinna mieć ramiona skierowane w dół. więc rozwiązanie tej nierówności to x∊(−∞,3>∪<4,+∞) i D=R/{3}. zatem rozwiązaniem tej wyjściowej nierówności jest x∊(−∞,3)∪<4,+∞)

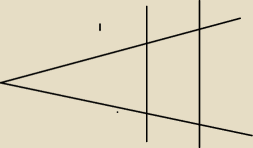
Marysia: 2. Wyznacz a i podaj Twierdzenie Talesa.

Marysia: nie wiem jak się pisze na obrazku. Ktoś podpowie? To poprawie

Marysia: On zakończył zadanie tamto tak:(−x+4)(x−3)≤0 I co dalej powinno być?

bezendu: @Marysia https://matematykaszkolna.pl/strona/533.html tu jest rozwiązanie do Talesa a gdzie Twoja inicjatywa

bezendu: A Kaja Ci dokończyła specjalnie nie podał Ci wyniku, żeby zmusić Cie trochę do myślenia...

Marysia: mogłabyś narysować mi ten wykres?

Marysia: przy pierwszej kresce u góry jest a, niżej jest 10. Przy drugiej kresce jest 2 i niżej 6. Nie wiem jak to na wykresie napisać

Kaja:

a		2
	=
10		6

6a=20 a=¹⁰₃ a Tw. Talesa poszukaj w książce do matematyki

Marysia: 1. Oblicz pole i obwód trapezu równoramiennego, w którym podstawy mają 1,2dm i 6cm, a ramiona 5cm. Obw = 1,2 + 5 + 6 + 5 = 17,2 cm P = (1,2+6)*4 przez 2 = 28,8 przez 2 = 14,4 cm² Czy ktoś mi powie czy to jest dobrze

Marysia: Wykonaj wskazane działanie.... Wiesz może jak to zrobić?

Kaja: jest źle. zauważ, że nie wszystkie długości boków sa podane w tych samych jednostach. zamień dm na cm.

Marysia: Czyli jak?

Marysia: czyli: 1,2dm + 5cm + 6cm + 5cm = 17,2?

Marysia: jak ja mam to teraz zamienić?

Kaja: 1 dm=10 cm więc 1,2 dm=12cm. do tych swoich wyliczeń zamiast wstawiać 1,2 wstaw 12.

Marysia: aha czyli będzie tak: Obw = 12cm + 5cm + 6cm + 5cm = 28cm P = (12+6)*4 przez 2 = 72 przez 2 = 36cm² Teraz dobrze?

Kaja: tak. dobrze.

Marysia: fajnie, dzięki. A pomożesz z tamtymi zadaniami jeszcze co wysłałam?

Marysia: 1. Zbadaj monotoniczność ciągu a_n = n² − n + 1

	2x−5
2. Rozwiąż równanie:		=x
	x−4

Marysia: i to u góry jeszcze jedno zadanie

Kaja: 1. a_n+1=(n+1)²−(n+1)+1=n²+2n+1−n−1+1=n²+n+1 a_n+1−a_n=n²+n+1−(n²−n+1)=n²+n+1−n²+n−1=2n>0 dla n∊ℕ₊ zatem ciąg jest rosnący

bezendu: a_n+1=(n+1)²−(n+1)+1=... a_n+1−a_n=.....

2x−5
	=x
x−4

D=ℛ\{4} 2x−5=x²−4x 2x−5−x²+4x=0 −x²+6x−5=0 policz Δ

Kaja: 2. zał.x≠4

2x−5
	=x /*(x−4)
x−4

2x−5=x²−4x x²−6x+5=0 Δ=36−20=16 √Δ=4

	6−4		6+4
x1=		=1 x2=		=5
	2		2

Marysia: a ten przykład : wykonaj wskazane działanie? Tam wyżej jest

Kaja:

	a		2y4		2ay4
=		*		=
	x		3b		3bx

Marysia: 1. Ile wyrazów ujemnych ma ciąg a_n = n² −2n − 24

	2x		x−1
2. Rozwiąż równanie:		−		=0
	2x+2		x+1

	2		6
3. Rozwiąż równanie:		+		=4
	x+1		x+3