Prawdopobobieństwo
Tina:
Błąd w rozwiązaniach ?
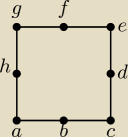
Dany jest kwadrat ACEG o polu 1. Ze zbioru wierzchołków kwadratu i środków jego boku(B,D,F,H)
losujemy trzy punkty:
oblicz prawdopodobieństwo:
c) wylosowane punkty wyznacza trójkat o polu 1/2
Nie wiem jak Wy i jak autor książki (testy maturalne aksjomat) ale ja tam widzę trochę więcej
tych trójkątów...
| | 1 | |
Żeby pole było równe jeden: P= |
| *a*h ⇒ a,h musi być równe 1, a takich trójkątów widzę |
| | 2 | |
8...
Po kolei ACD,CEG,EGA,GAC, ACF,CEH,GEB,GAD
Błąd w książce czy błąd mojego rozumowania
| | 4 | | 1 | | 8 | | 1 | |
Według rozwiązań wychodzi |
| czyli |
| a według mnie |
| czyli |
| , |
| | 56 | | 14 | | 56 | | 7 | |
z góry dzięki
5 kwi 19:00
Ajtek:
PΔACD≠1 już pierwszy Twój błąd.
5 kwi 19:06
Ajtek:
≠0,5 oczywiście
.
5 kwi 19:07
Tina: Oczywiście literówka i chodziło o ACE, czyli trójkątów tak czy siak jest 8...
5 kwi 19:15
Ajtek:
Może chodzi o Δ prostokątne.
5 kwi 19:18
Tina: Nie ma tego zaznaczonego w poleceniu, jest tylko
c) wylosowane punkty wyznacza trójkat o polu 1/2
Siedziałam nad tym i siedziałam, no i jak by nie patrzeć wychodzi jak wychodzi... Wzięłam tez
pod uwagę, ze Ω źle policzyłam, ale inne przykłady wyszły poprawnie czyli na pewno jest ok
5 kwi 19:33
Tina: I co z tym zadaniem, to jest błąd w książce?
5 kwi 19:55
Ajtek:
Wygląda na to, że tak. Może wcześniej w treści jest jakieś zastrzerzenie.
5 kwi 19:56
Tina: Oto cała treść zadania:
Dany jest kwadrat ACEG o polu 1. Ze zbioru wierzcholkow kwadratu i srodkow jego bokow losujemy
3 punkty.Oblicz prawdopodobienstwo, ze:
a) wylosowane punkty wyznacza trojkat
b) wylosowane punkty wyznacza trojkat ostrokatny
c) wylosowane punkty wyznacza trojkat o polu
a i b zrobiłam poprawnie.
Żeby było zabawniej.... następne w kolejności zadanie chyba też błąd
Niech
x−3 dla −3≤x≤2
f(x)= mx+1 dla 2<x≤7
Wyznacz wartość parametru m tak aby wykresem funkcji była łamana. Dla wyznaczonej wartości
parametru m:
a) wyznacz wykres funkcji:
b) zapisz wzór funkcji z użyciem wartości bezwzględnej
Autorowi jakimś cudem wychodzi takie V a mi wychodzi odwrócone V czyli takie /\ ....
Myślałam, że aksjomat to szanujące się wydawnictwo a tu niemałe zaskoczenie...
O ile co do
1 to jestem pewna, że to błąd w książce to co do 2 to nie wiem, dlatego proszę o sprawdzenie
5 kwi 20:10
Ajtek:
Na pewno to nie będzie V, czyli błąd.
5 kwi 20:15
Tina: Chyba ktoś trochę zapił przy układaniu tych zadań
Dzięki za pomoc.
5 kwi 20:27