kąt ostry Aloha: kąt α jest ostry i tgα=2. oblicz wartość wyrażenia 2cosα²−1

krystek: =sin²x=(U{2}{√5])²=

Aloha: trochę trudno mi to zrozumieć, skąd wyznaczyło się boki trójkąta?:

Fizyk:

	sinx
musisz rozwiazac uklad rownan :		=2 i sin2x + cos2x=1 <−−− jedynka
	cosx

trygonometryczna.

krystek:

	2
α jest ostry tgα=
	1

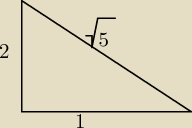
Artur_z_miasta_Neptuna: jak to skąd ... masz tgx = 2 no to wiesz że jedna przyprostokątna jest dwa razy dłuższa od drugiej ... niech ta mniejsza =1 to druga =2 z tw. pitagorasa liczysz przeciwprostokątną i po problemie

Aloha: dalej nie mogę tego obliczyć. Te dwa równania trzeba do siebie przyrównać i wyznaczyć cosx?

Artur_z_miasta_Neptuna: Aloha ... masz narysowany trójkąt i podane wartości kątów ... wyznaczasz z rysunku wartość cosα później podnosisz ją do kwadratu i odejmujesz 1 i już masz wartość szukanego wyrażenia

Aloha: aa ok, już rozumiem

krystek: Zależy , jeżeli sposobem Fizyka to tak

Fizyk: Tak jak sie rozwiazuje uklad rownan

sinx		sinx
	=2 , wiec sinx= 2 cosx, wiec cosx=
cosx		2

	sinx
sin2x+cos2x=1, wiec podstawiamy za cosx=
	2

	sin2x
sin2x+		=1
	4

5
	sin2x=1
4

	4
sin2x=
	5

	2
sinx=
	√5

zrozumiane?

Aloha: czyli rozwiązaniem jest −(4/5)?

Fizyk:

	4
nieeee rozwiazaniem jest U{2}{√5 ,		to kwadrat sinx, wiec musisz spierwiastkowac,
	5

przeciez Ci rozpisalam laadnie

Fizyk:

	2
*
	√5

Aloha: a jak wyszło ⁵₄ sin²x=1 bo sie już pogubiłam

pigor: ..., kąt α jest ostry i tgα=2; oblicz wartość wyrażenia 2cosα2−1 no to może chcesz np.... tak :

	cos2α		2cos2α
2cos2α−1= 2*		−1=		−1=
	1		sin2α+cos2α

	2cos2α		2		2		2		3
=		−1=		−1=		−1=		−1= −		=−0,6 .
	cos2α (tg2α+1)		tg2α+1		22+1		5		5

krystek: Oj Pigor teraz dopiero będzie zagwozdka dla Aloha.

krystek:

	1		2		3
2cos2α−1=2*(		)2−1=		−1=−		=−0,6
	√5		5		5

pigor: ..., no to jeszcze np, tak : niech k∊R₊ , więc

	sinα		2
tgα=2 ⇒		=		⇒ sinα= 2k icosα= k, ale sin2α+cos2α=1,
	cosα		1

to (2k)²+k²=1 ⇔ 4k²+k²= 1 ⇔ 5k²= 1 ⇒ k²=¹₅= cos²α , zatem 2cos²α−1= 2*¹₅−1= ²₅−⁵₅= −³₅= −0,6 . ...

Aloha: aaa, bo zapomniałam jeszcze odjąć 1 od ²₅ dlatego mi nie wychodziło, dziękuje