wielomian 4 stopnia zombi: Wyznacz wszystkie pary (p,q) liczb pierwszych, dla których równanie x⁴−px³+q=0 ma pierwiastek całkowity. Jakieś sugestie? Nie wiem czym to atakować Ferrari, czy jakoś prościej. Proszę hinty z góry dziękuję.

zombi: + ICSP jak będziesz, możesz rzucić jakimiś przykładami wielomianów, żeby Cardano albo Ferrari użyć? Byłbym wdzięczny

Eta: (3,2) ; (2,3)

a: Pierwiastek całkowity jest jednocześnie wymierny, a z twierdzenia o wymiernych pierwiastkach wielomianu wiemy, że możliwe x muszą być postaci: x ∊ { 1, −1, q, −q } (liczby pierwsze są podzielne tylko przez 1 i przez siebie) Wszystkie z nich są całkowite. Sprawdźmy zatem kiedy nasi kandydaci są naprawdę pierwiastkami. Z definicji pierwiastek wielomianu mamy gdy W(x) = 0. Zatem: W(1) = 1−p+q = 0 → p = 1+q ⇔ p = 3, q = 2 W(−1) = 1+p+q ≠ 0 → brak rozwiązań W(±q) = q⁴ − (±p)q³ + q = q(q³ − (±p)q² + 1) = 0 Ale q≠0, gdyż liczba 0 nie jest pierwsza, skąd mamy: (±p)q² = q³ + 1

	q3+1		1
p = ±		= ±(q +		) → brak rozwiązań dla dowolnej liczby pierwszej q
	q2		q2

Odpowiedź: (3,2)

zombi: O kurcze takie szprytne coś , a mógłbym prosić o jakiś wielomian 3 stopnia najlepiej do rozwalenia?

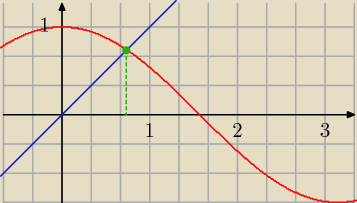
a: To może dam zadanie praktyczne. Znaleźć przybliżone rozwiązanie równania cos(x) = x. (x = 0.73908513321516064166...)

	x2
1. Korzystając z przybliżenia cos(x) ≈ 1 −
	2

	x2		x4
2. Korzystając z przybliżenia cos(x) ≈ 1 −		+
	2		24