Geometria
Damian17: Pomocy proszę

w trójkacie prostokątnym spodek wysokości, poprowadzonej z wierzchołka kąta prostego, podzielił
przeciwprostokątną na odcinki długości 1cm i 9cm. Oblicz sumę długości przyprostokątnych tego
trójkąta...
7 wrz 19:31
Damian17: Pomoże mi ktoś bardzo proszę

7 wrz 19:41
Damian17: chyba dzisiaj nikt nie pomaga na forum, a szkoda...
7 wrz 19:44
anoiłeczek: masz może rysunek przykładowy tego zadania

?
7 wrz 19:48
Damian17: niee
7 wrz 19:49
Damian17: bo on podzieli chyba je w punkcie prostym 90 stopni tak mi się wydaje, jest pod kątem prosty
względem do przeciwprostokątnej
7 wrz 19:51
anoiłeczek:
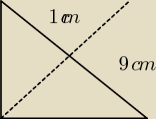
7 wrz 19:53
Damian17:

no może nie perfekcyjnie ale tak sobie na brudno narysowałem i wydaje mi się że ten mały to
będzie równoramienny czyli każdy bok po 1 cm, więc podstawa może mieć 1 cm? nie wiem co o tym
sądzicie?
7 wrz 19:54
anoiłeczek: moment
7 wrz 19:54
tim: Ja również myślę.
7 wrz 19:55
Damian17: wydaje mi się że ta prosta przetnie przeciwprostokątną pod kątem prostym i wtedy powstanie
równoramienny
7 wrz 19:55
Damian17: okey, dzięki z góry
7 wrz 19:56
tim: Tłumaczę.
7 wrz 19:57
anoiłeczek: mieliście już sinusy


7 wrz 19:57
anoiłeczek: bo wydaje mi się że to można by tak wyliczyć...
7 wrz 19:58
Damian17: noo były, proponuj
7 wrz 19:59
Damian17: Tim też daj swoje rozwiązanie

7 wrz 20:00
tim:

Korzystając z ukochanego podobieństwa trójkątów kąt, kąt, kąt obracamy sobie w wyobraźni
trójkąt z bokiem 1 i dochodzimy do wniosku, że bok AB musi być podobny do AD. Zatem
AB = k * AD (k = skala)
To samo z trójkątem CBD. Jest on podobny do ABC. Po obróceniu w wyobraźni widzimy, że bok CD
jest podobny do BC. Zatem:
BC = k * CD
Z tw. Pitagorasa:
(1k)
2 + (9k)
2 = (9 + 1)
2
k
2 + 81k
2 = 100
82k
2 = 100
k = U{10}{
√82
Można usunąć niewymierność.
Mamy skalę.
Mamy obliczyć AB + BC.
| | 100 | | 100√82 | |
AB + BC = 1k + 9k = 10k = |
| = |
| |
| | √82 | | 82 | |
7 wrz 20:02
Damian17: noo a mam wynik w odpowiedziach 4√10cm
7 wrz 20:09
Damian17: Aaa anoiłeczek miała jakąś propozycję czekam, choć to co rozwiązał ti trzyma się wszystkiego,
tylko że ten wynik w odpowiedziach

7 wrz 20:16
Damian17: ii jak? myśli ktoś dalej nad tym czy daje sobie spokój?
7 wrz 20:21
tim: Moment. Zaczynaja sie schodzić mistrzowie...
7 wrz 20:30
Bogdan:

Korzystamy z twierdzenia o wysokości w trójkącie prostokątnym opuszczonej z wierzchołka
kąta prostego (zielony trójkąt): h
2 = xy, czyli h jest średnią geometryczną odcinków x, y.
W tym zadaniu: h
2 = 1*9 i h > 0 ⇒ h =
√9 = 3
a >0, b > 0.
Z twierdzenia Pitagorasa w trójkącie BDC: a =
√1 + 9 =
√10
Z twierdzenia Pitagorasa w trójkącie ADC: b =
√81 + 9 =
√90 = 3
√10
Odp.: a + b =
√10 + 3
√10 = 4
√10
i to tyle.
7 wrz 20:30
tim: Bogdanie, gdzie mam błąd?
7 wrz 20:30
Damian17: Aaa spoko zaczekam

tylko żebym dostal odpowiedź
7 wrz 20:31
Damian17: noo bardzo dziękuję

7 wrz 20:32
Damian17: wiedziałem że tutaj jest zawsze na kim polegać

7 wrz 20:32
anoiłeczek: bogdanie może podał byś mi wskazówki do mojego zadania

7 wrz 20:38
7 wrz 20:41
tim: Tzn one są podobne. Kąt alfa, kąt prosty, kąt 90 stopni.
7 wrz 20:43
tim: Tfu kąt beta (ostatni).
7 wrz 20:43
Bogdan:
Timie, nie boki są podobne, ale trójkąty są podobne. W trójkątach podobnych odpowiadające
sobie boki są proporcjonalne (ale nie podobne).
7 wrz 20:50
tim: No dobrze, ale dalej nie wiem, czemu wyniki się różnią.
7 wrz 20:51
Bogdan:
Później Timie sprawdzę Twoje rozwiązanie.
7 wrz 20:58
tim: Ok, wiem już.
Rysunek i pomysł dobry, ale dalej:
h
2 = 9
h = 3
Zatem
stosunek boków AB / BC = 1/3
I wynik wychodzi 4
√10
7 wrz 21:06
 w trójkacie prostokątnym spodek wysokości, poprowadzonej z wierzchołka kąta prostego, podzielił
przeciwprostokątną na odcinki długości 1cm i 9cm. Oblicz sumę długości przyprostokątnych tego
trójkąta...
w trójkacie prostokątnym spodek wysokości, poprowadzonej z wierzchołka kąta prostego, podzielił
przeciwprostokątną na odcinki długości 1cm i 9cm. Oblicz sumę długości przyprostokątnych tego
trójkąta...

 ?
?

 no może nie perfekcyjnie ale tak sobie na brudno narysowałem i wydaje mi się że ten mały to
będzie równoramienny czyli każdy bok po 1 cm, więc podstawa może mieć 1 cm? nie wiem co o tym
sądzicie?
no może nie perfekcyjnie ale tak sobie na brudno narysowałem i wydaje mi się że ten mały to
będzie równoramienny czyli każdy bok po 1 cm, więc podstawa może mieć 1 cm? nie wiem co o tym
sądzicie?



 Korzystając z ukochanego podobieństwa trójkątów kąt, kąt, kąt obracamy sobie w wyobraźni
trójkąt z bokiem 1 i dochodzimy do wniosku, że bok AB musi być podobny do AD. Zatem
AB = k * AD (k = skala)
To samo z trójkątem CBD. Jest on podobny do ABC. Po obróceniu w wyobraźni widzimy, że bok CD
jest podobny do BC. Zatem:
BC = k * CD
Z tw. Pitagorasa:
(1k)2 + (9k)2 = (9 + 1)2
k2 + 81k2 = 100
82k2 = 100
k = U{10}{√82
Można usunąć niewymierność.
Mamy skalę.
Mamy obliczyć AB + BC.
Korzystając z ukochanego podobieństwa trójkątów kąt, kąt, kąt obracamy sobie w wyobraźni
trójkąt z bokiem 1 i dochodzimy do wniosku, że bok AB musi być podobny do AD. Zatem
AB = k * AD (k = skala)
To samo z trójkątem CBD. Jest on podobny do ABC. Po obróceniu w wyobraźni widzimy, że bok CD
jest podobny do BC. Zatem:
BC = k * CD
Z tw. Pitagorasa:
(1k)2 + (9k)2 = (9 + 1)2
k2 + 81k2 = 100
82k2 = 100
k = U{10}{√82
Można usunąć niewymierność.
Mamy skalę.
Mamy obliczyć AB + BC.

 Korzystamy z twierdzenia o wysokości w trójkącie prostokątnym opuszczonej z wierzchołka
kąta prostego (zielony trójkąt): h2 = xy, czyli h jest średnią geometryczną odcinków x, y.
W tym zadaniu: h2 = 1*9 i h > 0 ⇒ h = √9 = 3
a >0, b > 0.
Z twierdzenia Pitagorasa w trójkącie BDC: a = √1 + 9 = √10
Z twierdzenia Pitagorasa w trójkącie ADC: b = √81 + 9 = √90 = 3√10
Odp.: a + b = √10 + 3√10 = 4√10
i to tyle.
Korzystamy z twierdzenia o wysokości w trójkącie prostokątnym opuszczonej z wierzchołka
kąta prostego (zielony trójkąt): h2 = xy, czyli h jest średnią geometryczną odcinków x, y.
W tym zadaniu: h2 = 1*9 i h > 0 ⇒ h = √9 = 3
a >0, b > 0.
Z twierdzenia Pitagorasa w trójkącie BDC: a = √1 + 9 = √10
Z twierdzenia Pitagorasa w trójkącie ADC: b = √81 + 9 = √90 = 3√10
Odp.: a + b = √10 + 3√10 = 4√10
i to tyle.
 tylko żebym dostal odpowiedź
tylko żebym dostal odpowiedź


