4 kwi 21:23
henio: up
4 kwi 23:20
henio: up
5 kwi 00:27
PW: Nie przekonałeś mnie. Trzeba wykorzystać informacje o długościach krawędzi podstawy do
wyliczenia długości krawędzi bocznych i skorzystać z twierdzenia odwrotnego do twierdzenia
Pitagorasa. W oznaczeniach na rysunku widzę taki pomysł, ale niewykorzystany. Stwierdzenia o
rzutach nie wystarczą, nie rozumiem skąd wnioski.
5 kwi 01:09
Mila:
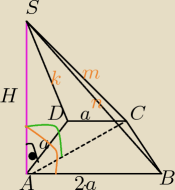
AS prostopadła do płaszczyzny ABCD jako wysokość ostrosłupa, z treści zadania,
⇔AS⊥AB, AS⊥AD, AS⊥AC
AC=a
√2, BC=a
√2 ( to obliczyłeś)
Masz 3 Δprostokątne: ΔSAB,ΔSAD,ΔSAC
Trzeba uzasadnić, że :
ΔSDC i ΔSCB są prostokątne:
WΔSAD: k
2=
H2+a2
W ΔSAC:
m
2=H
2+(a
√2)
2=
H2+2a2
W ΔSDC:
m
2=?k
2+a
2⇔
H2+2a2=?
H2+a2+a
2=H
2+2a
2, L=P na podstawie tw. odwrotnego do tw.
Pitagorasa ΔSDC jest prostokątny
Dokończ.
5 kwi 14:52
henio: dokończyłem− dziękuję
Dlaczego mój dowód nie jest poprawny?
6 kwi 15:11
