matematykaszkolna.pl
RÓWNOLEGŁOBOK !!!!!!!!!!!!!! V.Abel:
 1 
Jak udowodnić/wyprowadzić wzór na pole równoległoboku: P=
d e sinα, gdzie d,e to
 2 
przekątne? ? ? POMOCY
4 kwi 21:17
V.Abel: α to kąt między przekątnymi
4 kwi 21:20
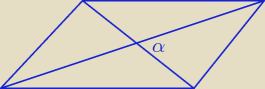Godzio: rysunek Mamy 4 trójkąty. Przekątne (d i e) dzielą się na pół. Pole każdego z tych trójkątów to:
 1 1 1 1 1 1 
2 *
*
e *
d * sinα + 2 *
*
e *
d * sin(180o − α) =
 2 2 2 2 2 2 
1 1 
edsinα +
edsin(180o − α), ale sin(180o − α) = sinα więc otrzymujemy tezę
4 4 
4 kwi 21:21
V.Abel: Aha...dzięki, to jest jedyny dowód na to twierdzenie? emotka . istnieje może inny?. . p.s. dzięki wielkie
4 kwi 21:23
Godzio: Można wektorami na pewno. Inny w tej chwili nie przychodzi mi do głowy.
4 kwi 21:26
V.Abel: Ok, dzięki wielkie emotka Analogicznie można dla każdego czworokąta? W sensie, dowolnego i też wyjdzie? ? ?
4 kwi 21:29