geometria L.: Mam zadanie: oblicz pole trapezu majac dane dlugosci podstaw a,b i dlugosci ramion c,d. a=11cm b=6cm c=12cm d=13cm Mam taki poczatek rozwiazania: (a−b),c,d 5,12,13 5²+12²=13² − czyli trapez prostokatny Moze mi to ktos wytłumacyc?

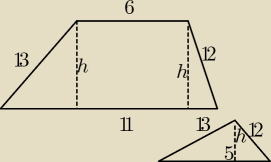
Michał: z tego trójkąta wyliczyć h np z wzoru herona i zadanie teoretycznie skończone

Michał: @Mam taki poczatek rozwiazania: (a−b),c,d 5,12,13 5²+12²=13² − czyli trapez prostokatny Niestety to nie jest poprawne ponieważ to trapez różnoramienny.

L.: a możesz zmi wytłumaczyc ten poczatek rozwiazania,ktore mialam w zeszycie? i gdybym chciala podazac twoim sposobem to co to jest wzor herona?

Michał: no to po kolei. sugerując sie rysunkiem i twoim początkiem rozwiązania nie można powiedzieć że jest to trapez prostokątny. co do wzoru herona, to skoro go nie znasz jeszcze to nie wiem czy możesz go używać niestety mi nic innego do głowy nie przychodzi jak to rozgryźć.

	1
wzór herona p=		(a+b+c) − połowa dł. obwodu
	2

Wtedy S− pole > S=√p(p−a)(p−b)(p−c) podstawiasz boki tego trójkąta do wzoru i liczysz pole

	1
Następnie wiadomo że pole to również		ah
	2

czyli S=5*h, a−podstawa mając h wyliczamy pole trapezu

Michał: dla jasności wzór herona to : S=√p(p−a)(p−b)(p−c) , tam tego nie zaznaczyłem jednoznacznie

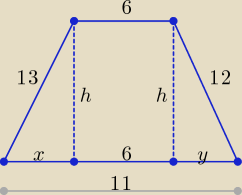
Bogdan: x + 6 + y = 11 ⇒ x + y = 5 h² + x² = 169 h² + y² = 144 − −−−−−−−−−−− x² − y² = 25 ⇒ (x + y)(x − y) = 25 ⇒ 5(x − y) = 25 ⇒ x − y = 5 Trzeba rozwiązać układ równań: x + y = 5 i x − y = 5, potem można obliczyć długość h

L.: x2 − y2 = 25 ⇒ (x + y)(x − y) = 25 ⇒ 5(x − y) = 25 ⇒ x − y = 5 Nie rozumiem tego kroku.. PS.Mam kłopoty z geometrią,proszę o cierpliwość

Michał: x²−y²=25 >(x−y)(x+y)=25 jest to wzor skroconego mnozenia a pozniej jest podstawienie za x+y=5 do rownania i podzielenie stronami przez 5. odwolujac sie do tego co wczoraj podalem. ten trapez jest rzeczywiscie prostokatny, ale nie mozna bylo tego wykazac na podstawie twojego zapisu. z obliczen bogdana wyjdzie ze y=0 −> ze x=5 i z tw pitagorasa w tym trapezie mozna obliczyc wysokosc ktora wynosi 12 ponadto zawiera sie w jednym z ramion. patrzac na trojkat ktory wczoraj stworzylem z tw odwrotego do pitagorasa mozna tez to latwo wykazac i nie trzeba kozystac z wzoru herona.