Wyznacz miarę kąta między ścianą boczną a płaszczyzną podstawy. PILNE! Zdezorientowana;): Hejka. Krawędź podstawy ostrosłupa prawidłowgo trójkątnego jest równa 6, a jego objetość jest równa 9√3 cm³. Wyznacz miarę kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa oraz oblicz jego pole. Czy ktoś może mi zadania tego typu?

Zdezorientowana;): Czy ktoś może mi WYTŁUMACZYĆ zadania tego typu?

Zdezorientowana;): Czy ktoś może mi WYTŁUMACZYĆ zadania tego typu?

Karolina: kojarzysz czy ostroslp prawidlowy ma w podstawie trojkat rownoboczny? xD

Karolina: juz ci pisze

Karolina: o ile prawidlowy ma trojkat rownoboczny xD

Zdezorientowana;): Na podstawie objętości ostrosłupa obliczyłam, że H (wysokość ostrosłupa) ma 3. Ze wzoru na wysokość podstawy (a√3/2) wyszło mi 3√3. Co dalej?

Zdezorientowana;): tak, ma... równoboczny w podstawie i 3 równoramienne jako ściany boczne

Gromo: Ostrosłup prawidłowy trójkątny ma w podstawie trójkąt równoboczny.

Tomek:

	6√3
h=		=3√3
	2

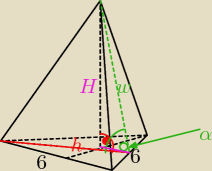
odcinek fioletowy nazwijmy go x:

	1
x=		*h=√3
	3

	1
V=		*Pp*H
	3

	62P{3}
Pp=		= 9√3
	4

V=9√3

	1
9√3=9√3*		*H => H=3
	3

w− wysokość ściany bocznej: (twierdzenie pitagorasa) 9+3=w² w=2√3 szukany kąt to α:

	H
tgα=		= √3
	1/3h

α=60^o

	6*w
Pc= (		)*3 +Pp
	2

chyba sb juz poradzisz powinno byc dobrze

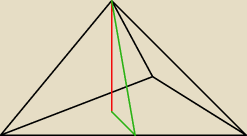
Gromo: Kolor czerwony − wysokość. Kolor Zielony − kąt szukany w zadaniu. "Oblicz jego pole" − mowa o powierzchni całkowitej?

Karolina: V− objetosc Pp− pole podstawy czyli Δ równobocznego h−wysokosc ostroslupa a− bok podstawy czyli ta krawędzi równa 6

	1
V=		* Pp * h
	3

wzor na pole trójkąta rownobocznego

	a2√3
P=
	4

	36√3
P
	4

co po skroceniu daje P=9√3 Podstawiamy dane do wzoru na pole trojkąta P=U{6²√3{4} Przypominam,ze V=9√3 Podstawiamy do wzoru na objętoś

	1
9√3=		*9√3*h
	3

Zdezorientowana;): tak. Czyli pp+pb

Karolina: Tomek dobrze napisal

Zdezorientowana;):