3p{x}-x-3=0 Clifford: Witam, mam do rozwiązania takie równanko. Rozwiązuje je na dwa sposoby i wychodzą mi dwa różne wyniki. Prosze o nakierowanie. Szukam x wierzchołka. RÓWNANIE :3√x−x−3=0 I sposób 3√x=x+3 // podnosze do kwadratu 9x=x² + 6x +9 0 = x² −3x + 9 x_w = 3/2 II sposób 3√x−x−3=0 t= √x 3t − t² − 3 = 0 // *(−1) t² − 3t +3 = 0 t_w = 3/2 czyli => 3/2 = √x // do kwadratu x = 9/4 Podsumowywując wychodzą mi dwa rózne wyniki x= 3/2 i x = 9/4 Prosze o pomoc.

Clifford: Ma ktoś jakiś pomysł ?

Bogdan: Zapiszmy równianie tak: −x + 3√x − 3 = 0 i x≥0, Δ = 9 − 12 < 0 brak rozwiązaniua

Clifford: Ale ja szukam wierzchołka

Bogdan: Jakiego wierzchołka? Przecież to jest równanie, a nie zapis wzoru funkcji.

Clifford:

	7
wyszedłem z tej funkcji: f(x) =		|3√x−x−3|
	2

	7
czyli f(x)=		|x−3√x+3| delta funkcji pod modułem jest mniejsa od zera
	2

	7
f(x)=		(x−3√x+3) i tutaj dochodze do tego ze mój pierwszy sposób był nimożliwy do
	2

użycia bo jak napisałes nie ma miejsc zerowych więc porównanie (x−3√x+3) do 0 nic by mi nie dało. Dzięki

Clifford: Temat uznaje za zakończony. Jeszcze raz wielkie dzięki Bogdan

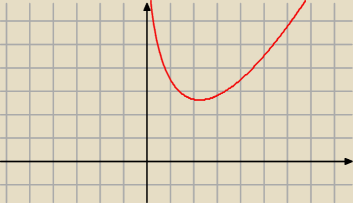
Bogdan: W tym przypadku dla wszystkich wartości x∊R funkcja przyjmuje wartości dodatnie. Metodami analizy matematycznej (obliczając pochodną funkcji) można wyznaczyć ekstremum funkcji.

	9
Rysunek przedstawia wykres Twojej funkcji, funkcja posiada minimum dla x =
	4