geometria pinguin: Na kuli opisano stożek Stosunek pola podstawy stożka do pola powierzchni kuli wynosi 3:4 Oblicz stosunek objętości kuli do objętości stożka. Prosze o wyjasnienie zadania

Kipic:

	vk
wiec mamy stosunek
	Vs

P_{podstawy stozka}=πr² P_k=4πR²

Ppodstawy stozka		3
	=
Pk		4

πr2		3
	=
4πR2		4

12πR²=4πr² 3R²=r²

vk		4   πR3 3
	=
Vs		1   πr2h 3

vk		4   πR3 3
	=
Vs		1   π3R2h 3

vk		4   R 3
	=
Vs		h

pinguin: w odp jest 4/9 czemu? przeciez tu nie ma zadnych liczb

Kipic:

	4   R 3		4
bo jak dalej policzysz to okazuje sie ze h=3R wiec		=
	3R		9

Krzys: πr² /4πR² =r² /4R² = 3/4,zatem r² =3R² , gdzie r−promien podstawy stozka a R−promien kuli. Stosunek objetosci kuli do objetosci stozka: (4/3)πR³ /(1/3)πr²h = 4R³ /r² h = 4R/(3h). Popracuj nad zaleznoscia R od h.

pinguin: dzieki ludzie!

Bogdan:

πR2		3		R2		R
	=		⇒ πR2 = 3πr2 ⇒		= 3 ⇒		= √3 ⇒ R = r√3
4πr2		4		r2		r

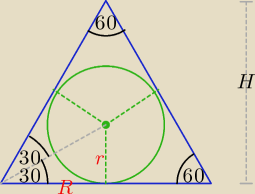
a więc przekrój osiowy stożka jest trójkątem równobocznym i H = 3r

	4		1		1
Objętość kuli Vk =		πr3, objętość stożka Vs =		*3πr2*3r =		*9πr3
	3		3		3

Vk		1   4* πr3   3		4
	=		=
Vs		1   9* πr3   3		9