rachunek prawdopodobieństwa xx: Może ktoś pomoże Zdarzenia A i B zawarte w zbiorze Ω spełniają warunek P(A) =3/5 i A⊂B. Wyznacz P (A∩B)?

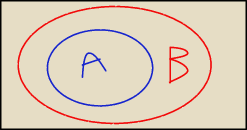
use: ja zawsze przy takich zadaniach posługuje się pomocniczym rysunkiem ; zobacz ;

	3
P(A)=		⇒ P(AnB)=P(A)
	5

use: zobacz na rysunku , jeżeli A zawiera się w B to ile wynosi A czesc wspolna z B

xx: Czyli B?

xx: Wiem czyli cześć wspólna A i B to A

use: nie B, zobacz jakiś mniejszy zbiór zawiera się w większym czyli A w B to ile wynosi częśc wspólna ( czyli inaczej gdzie te zbiory się ze sobą pokrywają ) z rysubku wynika że tu gdzie jest A bo A zawiera się w b czyli A czesc wspolna z B to po prostu A

xx: Dzięki za pomoc

use: jak masz takie zadania to zawsze rusuj sobie pomocniczo , pomaga jak sie nie ma wyobrazni takiej

xx: Tak wiem dziękuje coś mnie zaćmilo dziś.

Krzys: Jak moze byc B, jesli prosza o znalezienie P(A n B)? Czesc wspolna A z B rowna sie mniejszemu z nich, czyli rowna sie A. Zatem prawdopodobienstwo tego zdarzenia (A n B) jest rowne prawdopodobienstwu zdarzenia A. Stad P(A n B)=3/5.