rozwiaż hejloł: ||x−1|−|3−x||=2 jak to rozwiązać?

Pioterek08: ||x−1|−|3−x||=2 rozpisujemy na alternatywę rozwiązań |x−1|−|3−x|=2 ∨ |x−1|−|3−x|=−2 szukasz miejsca zerowe dla y=x−1 oraz y=−x+3 , najlepiej narysować obie funckje na wykresie i odczytujesz znaki w danych przedziałach i opuszczasz moduł x∊(−∞:1) −(x−1)−(3−x)=2 −x+1−3+x=2 0=4 sprzeczność x∊<1:3) (x−1)−(3−x)=2 x−1−3+x=2 2x=6 x=3 x∊<3:+∞) (x−1)+(3−x)=2 x−1+3−x+2 0=4 sprzeczność z trzech przepadków rozwiązanie jedno x=3 analogicznie dla sytuacji gdy |x−1|−|3−x|=−2 x∊(−∞:1) −(x−1)−(3−x)=−2 −x+1−3+x=−2 0=0 tożsamość więc chyba x∊(−∞:1) x∊<1:3) (x−1)−(3−x)=−2 x−1−3+x=−2 2x=2 x=1 x∊<3:+∞) (x−1)+(3−x)=−2 x−1+3−x=−2 0=−4 sprzeczność tutaj masz dwa rozwiązania x∊(−∞:1) ∧ x=1 sumując x∊(−∞:1> biorąc dwa przypadki pod uwagę x∊(−∞:1> ∨ x=3 mogę się mylić, więc proszę o sprawdzenie mojego rozumowania

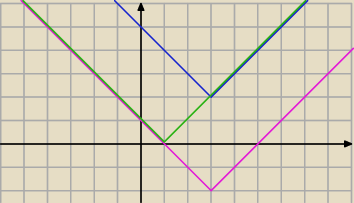
aniabb: odp x∊(−∞;1> u <3;∞)

hejloł: w odpowiedzi jest x∊(−∞,−1>u<3,+∞)

aniabb: w książkach też zdarzają się literówki