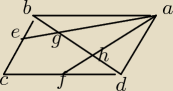
 ICFI=IFDI i ICEI=IBEI, udowodnij IBGI=IGHI=IHDI
ICFI=IFDI i ICEI=IBEI, udowodnij IBGI=IGHI=IHDI
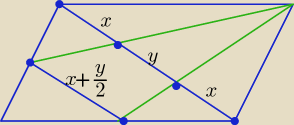 Wskazówki są na rysunku.
Wskazówki są na rysunku.

 ?
?

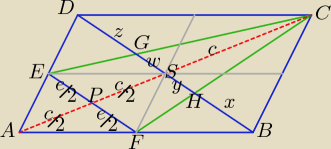 No cóż, czasami nie wystarczy godzina, a nawet dwie godziny, żeby wpaść na pomysł rozwiązania
zadania.
e = z + w = x + y
Z podobieństwa trójkątów: EPC i GSC:
No cóż, czasami nie wystarczy godzina, a nawet dwie godziny, żeby wpaść na pomysł rozwiązania
zadania.
e = z + w = x + y
Z podobieństwa trójkątów: EPC i GSC:
|
| 1 | 1 | 2 | |||||||||||||||||
= | ⇒ w = | e i z = e − w = e − | e = | e | |||||||||||||||||
| w | c | 3 | 3 | 3 |
|
| 1 | 1 | 2 | |||||||||||||||||
= | ⇒ y = | e i x = e − y = e − | e = | e | |||||||||||||||||
| y | c | 3 | 3 | 3 |
| 1 | 1 | 2 | ||||
w = | e i y = | e ⇒ w + y = | e = x = z | |||
| 3 | 3 | 3 |
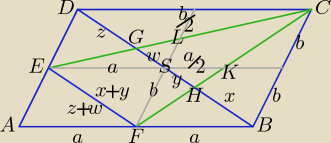 Drugie rozwiązanie.
x+ y = z + w
Drugie rozwiązanie.
x+ y = z + w
|
| ||||||||||||||||||
Z podobieństwa trójkątów: KEF i KSH: | = | ⇒ x = 2y | |||||||||||||||||
| x + y | y |
| 1 | ||
i x + y = 2y + y = 3y i y = | x | |
| 2 |
|
| ||||||||||||||||||
Z podobieństwa trójkątów: LEF i LGS: | = | ⇒ z = 2w | |||||||||||||||||
| z + w | w |
| 1 | ||
i z + w = 2w + w = 3w i w = | z | |
| 2 |
| 1 | 1 | 1 | 1 | 1 | 1 | |||||||
y = | x i w = | z ⇒ y + w = | x + | z = | x + | x = x = z | ||||||
| 2 | 2 | 2 | 2 | 2 | 2 |
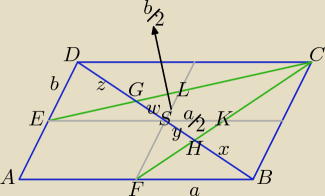 Trzecie rozwiązanie:
Trzecie rozwiązanie:
| a | x | 1 | ||||||||||
Z podobieństwa trójkątów: FBH i KSH: | = | ⇒ y = | x i x = 2y | |||||||||
| y | 2 |
| 1 | 3 | |||
x + y = 2y + y = 3y oraz x + y = x + | x = | x | ||
| 2 | 2 |
| b | z | 1 | ||||||||||
Z podobieństwa trójkątów: EDG i LSG: | = | ⇒ w = | z i z = 2w | |||||||||
| w | 2 |
| 1 | 3 | |||
z + w = 2w + w = 3w oraz z + w = z + | z = | z | ||
| 2 | 2 |
| 3 | 3 | |||
Z równości: x + y = z + w ⇒ 3y = 3w ⇒ y = w oraz | x = | z ⇒ x = z | ||
| 2 | 2 |
| 1 | ||
y + w = y + y = 2y = 2 * | x = x = z | |
| 2 |
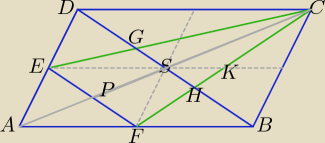 Czwarte rozwiązanie.
Wróćmy do pierwszego rysunku.
Odcinki EF i DB są równoległe.
|EF| = |BS| = |SD|
Przekątna AC zawiera środkową PC trójkąta EFC i środkową SC trójkąta GHC,
|EP| = |PF| i ze względu na równoległość EF i DB: |GS| = |SH|.
Czwarte rozwiązanie.
Wróćmy do pierwszego rysunku.
Odcinki EF i DB są równoległe.
|EF| = |BS| = |SD|
Przekątna AC zawiera środkową PC trójkąta EFC i środkową SC trójkąta GHC,
|EP| = |PF| i ze względu na równoległość EF i DB: |GS| = |SH|.
| 1 | ||
|GH| = y ⇒ |GS| = |SH| = | y | |
| 2 |
| 1 | ||
|EF| = |BS| ⇒ x + | y | |
| 2 |
| 1 | ||
oraz |SD| = |DG| + |GS| ⇒ |SD| = |DG| + | y, | |
| 2 |
| 1 | 1 | |||
|SD| = |BS| ⇒ |SD| = |DG| + | y i |SD| = x + | y ⇒ |DG| = x | ||
| 2 | 2 |
| 1 | ||
Z faktu: |KS| = | |FB| i z podobieństwa trójkątów FBH i KSH: | |
| 2 |
| |FB| | |HB| | |FB| | x | ||||||||||||||||
= | ⇒ | = | ⇒ x = y | ||||||||||||||||
| |KS| | |SH| |
|
|