Optymalizacja: Mamy 360m siatki ogrodzeniowej guest: Mamy 360m siatki ogrodzeniowej. Chcemy ogrodzić dwa jednakowe prostokątne obszary o wspólnym boku. Jak dobrać wymiary tych obszarów, aby ich pola były największe? Pomoże ktoś rozwiązać takie zadanie? Jest jakiś schemat jak postępować w tego typu zadaniach optymalizacyjnych, żeby w miarę prosto dało się je liczyć? Z góry dziękuję za wszelką pomoc.

Artur_z_miasta_Neptuna: są to dwie działki połączone bokiem ... działki są jednakowych wymiarów ... więc możesz to zadanie ropatrywać jako 'oplecenie' ogrodzeniem jednej (dużej) dzialki P = a*b Ob = 2a+2b = 360 → a = 180−b P = a*b = (180−b)*b = ... <−−− szukasz wierzchołka tejże paraboli

guest: dzięki

guest: a jednak nie dzięki:( ktoś pomoże to rozwiązać? czy tu chodzi ze wzorów na p i q wyliczyć współrzędne wierzchołka? p=−b/2a = 90 q=8100 i to raczej nie jest to anybody help?

guest: serio nikt?

guest: po wyznaczeniu xw=90 i wstawieniu tego do równania a=180−b a=90 czyli wyszłoby ze najwieksze mozliwe pole duzej działki to kwadrat o boku 90. Ale co z tym jednym bokiem, którym te dwie równe działki są złączone?

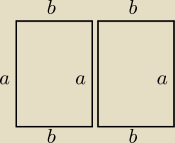
aniabb: podejrzewam że ten bok też ma być ogrodzony, ale wystarczy jedna siatka zatem 3a+4b=360 ⇒ b=90−0,75a Pole=ab − max Pole = a(90−0,75a) = −0,75a² + 90a parabola smutna max w wierzchołku

	−90
amax =		= 60
	−1,5

b= 90−0,75*60= 45

guest: bardzo dziękuję