Wykaż, że funkcje f oraz g nie są równe Hmm: Wykaż, że funkcje f oraz g nie są równe, jeśli: f(x) = √x² g(x) = (√x)²

ICSP: pokaż ze mają inne dziedziny.

Hmm: f(x) = √x² g(x) = (√x)² √x² = IxI (√x)²= x D= R D=R chyba coś pokręciłam

ICSP: jak widać Wiesz że dziedzinę ustala się przed wykonaniem jakichkolwiek przekształceń ?

Hmm: mój błąd więc: f(x) = √x² g(x) = (√x)² x² ≥ 0 tej nie potrafię x≥0 D= <0, ∞)

ICSP: widzę że obydwu nie potrafisz Popraw f a ja zrobię g g(x) = (√x)² D : x ≥ 0 ⇒ x ∊ <0 ; +∞) Jest tylko jeden pierwiastek a wartość pod pierwiastkiem musi być większa bądź równa 0

Hmm: f(x) = √x² D : x² ≥ 0 ⇒ x ≥ 0 ⇒ x ∊ <0 , ∞) wiem, to jest źle

ICSP: :( x² ≥ 0 − jest to podstawowa nierówność Poszukaj w zeszycie, albo książce wykresu funkcji x² i powiedz dla jakich x ten wykres leży na osią OX

Hmm: dla wszystkich oprócz x=0, wtedy y=0

ICSP: czyli x² ≥ 0 ⇒ x ∊ Tylko pamiętaj że równe tez może być

Hmm: x ∊ R ?

ICSP: f(x) = √x² , D : x ∊ R g(x) = (√x)² , D : x ∊ <0 ; +∞) Dziedziny nie są równe więc i funkcje nie są równe.

Hmm: mam jeszcze jeden przykład: f(x) = ( 1 ⇒ x ≥ 2 g(x) = sgn(x−2) ( −1 ⇒ x <2 tej nie potrafię D=R

use: przecież zgodnie z definicją √x²=(x²)^1₂=x

	1
analogicznie z drugim przykładem( tylko odwrotnie x jest w potedze		),a to jest wtedy
	2

równe, czyli mam rozumieć że w takich przypadkach z działaniami idziemy od środka?

ICSP: Najpierw ustalasz dziedzinę, a później dopiero możesz się bawić w różnego typu przekształcenia Co do drugiego przykładu wiesz co to jest funkcja signum ?

Hmm: dla dodatnich R 1, dla ujemnych −1, dla zera zero, coś takiego

use: sgn to z łaciny znak

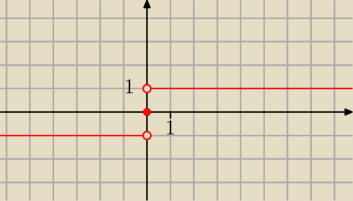
ICSP: "coś takiego" funkcja signum jest funkcją znaku. Wzór :

	⎧	1 gdy x > 0
sgn(x) =	⎨	0 gdy x = 0
	⎩	−1 gdy x < 0

Funkcja która może przyjąć 3 wartości i której dziedzina jest zbiór liczb rzeczywistych Teraz zastanów się dla jakiego punktu wartości funkcji f oraz g będą różne.

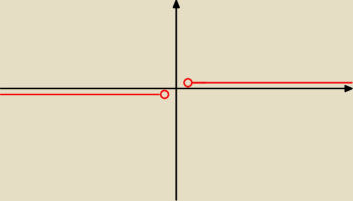
Hmm: myślę, myślę, ale dojść nie mogę, to byłoby f(x) = ( 1 ⇒ x ≥ 2 ( −1 ⇒ x <2

ICSP: ale masz pokazać że dla pewnego x wartości f oraz g są różne. Wystarczy znaleźć jeden x Zatem skoro singum przyjmuje 3 wartości a f przyjmuje tylko dwie. To logicznym byłoby pomyślenie dla jakiego x sgn przyjmie wartość której nie przyjmuje f

Hmm: 0

ICSP: ?

Hmm: funkcja f nie przyjmuje wartości 0

ICSP: a funkcja g przyjmuje. Znajdź x dla którego funkcja g przejmuje tą wartość i napisz że f(x) ≠ g(x) zatem funkcje nie są równe

ICSP: tylko w miejsce x wstaw odpowiednią cyferkę

Hmm: w funkcji g(x) x=0

ICSP: g(x) = sgn(x−2) g(0) = sgn(−2) = −1 chyba coś nie tak. Liczba −2 ma ujemny znak

Hmm: nie wiem

ICSP: wstawiaj kolejne liczby aż dojdziesz do zera albo zauważ że : 0 = sgn(0) i rozwiąż proste równanie liniowe

Hmm: g(x) = sgn(x−2) g(0) = sgn(−2) = −1 a jak uzyskałeś tę −1 ?

ICSP: mówiłem chodzi tutaj o znak. Czy liczba jest ujemna czy liczba jest dodatnia Jeżeli liczba jest ujemna wtedy znak tej liczby jest ujemny i przypisujemy jej wartość −1 Jeżeli jest dodatnia to wartość 1 sgn(5) = 1 bo 5 jest liczba dodatnia sgn(0) = 0 sgn(−5) = −1 bo −5 jest liczbą ujemną

Hmm: w funkcji g(x) x=1

ICSP: ?

Hmm: nie ogarniam

Hmm: nic mi nie pasuje

ICSP: :( to może najpierw rozróżnimy że sgn(x) nie jest równe sgn(x−2) Kiedy już to wiemy Wprowadzę sobie oznaczenia : f(x) = sgn(x) g(x) = sgn(x−2) i teraz najważniejsze. Zachodzi własność : g(x) = f(x−2). Skoro już wiesz jaka własność jest pomiędzy tymi dwoma funkcjami możesz postarać się narysować g(x) = sgn(x−2) czyli przesunąć f(x) = sgnx o dwie jednostki w prawo

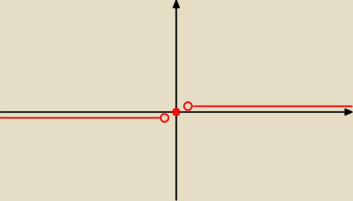
Hmm: g(x) = sgn(x−2)