geometria - Udowodnij
Pan Adam: Bardzo proszę o pomoc z tym zadaniem ponieważ siedzę nad nim od wczoraj i kompletnie nie mam
pomysłu na rozwiązanie.
TREŚĆ:
Udowodnić, że suma odległości dowolnego punku należącego do wnętrza wielokąta wypukłego o
bokach równej długości od prostych zawierających boki tego wielokąta jest stała.
Pozdrawiam,
Adam
3 kwi 13:28
Artur_z_miasta_Neptuna:
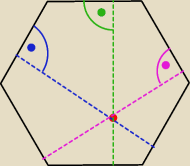
zadanie rozbijmy na dwa przypadki:
1) wielokąt ten posiada parzystą liczbę boków
2) posiada nieparzysta liczbę boków
(1) (rysunek dla 6 boków)
zauważasz, że w wielokącie foremnym o parzystej liczbie boków ... każdemu bokowi odpowiada
dokładnie jeden bok tej samej długości, równoległy do niego ... a więc odległość punktu
(leżącego pomiędzy nimi lub ich przedłużeniami) od obu tych boków będzie stala i będzie
wynosić dokładnie tyle ile wynosi odległośc pomiędzy tymi dwoma bokami
(2) w następnym poście
3 kwi 13:56
irena_1:
a− długość boku wielokąta
P− pole wielokąta
Są to wartości stałe dla danego wielokąta
d
1, d
2, ..., d
n − odległości punktu P− wewnętrznego wielokąta od jego boków
s=d
1+d
2+...+d
n
Jeśli poprowadzimy odcinki łączące punkt P z wierzchołkami wielokąta, to podzielą one wielokąt
na trójkąty, w których podstawami będą boki wielokąta, a odległości d
1, d
2,... d
n −
wysokościami tych trójkątów
| | 1 | | 1 | | 1 | | 1 | | 1 | |
P= |
| ad1+ |
| ad2+...+ |
| adn= |
| a(d1+d2+...+dn)= |
| as |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
Dla danego wielokąta suma odległości punktu wewnętrznego od boków wielokąta o równych bokach
jest stała.
3 kwi 13:58
irena_1:
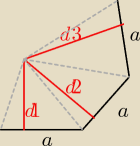
To "część" tego wielokąta
3 kwi 14:04
Artur_z_miasta_Neptuna:
kurdę ... przeciez to zadanie nie wymaga żadnej filozofii
wielokąt foremny o 'n' bokach można podzielić na 'n' trójkątów, o podstawie 'b' (bok wielokąta)
i jakiś różnych wysokościach h ... zauważmy, że odległości punktu P od boków wielokąta to nic
innego jak ów 'h' trójkątów.
Jako, że trójkąty dzielą całe pole wielokąta ... to suma pól tych trójkątów jest równa
czyli:
| | bh1 | | bh2 | | bhn | | b | |
PΔ1 + PΔ2+...+PΔn = |
| + |
| + ... + |
| = |
| (h1+h2+...+hn) = const. |
| | 2 | | 2 | | 2 | | 2 | |
c.n.w.
3 kwi 14:12
Pan Adam: Bardzo wam dziękuję za rozwiązania. Za moment zacznę je analizować.
Pozdrawiam,
Adam
3 kwi 15:34
Pan Adam:
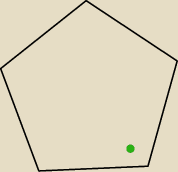
Ale co w przypadku jeżeli punkt będzie tutaj?
3 kwi 15:56
Pan Adam: Nie będzie on wtedy na linię wysokości trójkątów i mogę się mylić ale nie na każdy bok damy
radę poprowadzić linię pod kątem prostym co utrudnia sytuację
3 kwi 15:58
Pan Adam: Proszę o ustosunkowanie się do mojego problemu. Dziękuję
3 kwi 16:49
Pan Adam: Bardzo Proszę o odpowiedź. Nie daje mi to spokoju.
3 kwi 19:16
Pan Adam: ?
3 kwi 21:04
Pan Adam: ?
4 kwi 00:34
zombi:
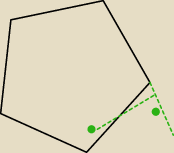
4 kwi 00:43
zombi: Jak przy rozwartych trójkątach jeśli o to ci chodziło
4 kwi 00:44
 zadanie rozbijmy na dwa przypadki:
1) wielokąt ten posiada parzystą liczbę boków
2) posiada nieparzysta liczbę boków
(1) (rysunek dla 6 boków)
zauważasz, że w wielokącie foremnym o parzystej liczbie boków ... każdemu bokowi odpowiada
dokładnie jeden bok tej samej długości, równoległy do niego ... a więc odległość punktu
(leżącego pomiędzy nimi lub ich przedłużeniami) od obu tych boków będzie stala i będzie
wynosić dokładnie tyle ile wynosi odległośc pomiędzy tymi dwoma bokami
(2) w następnym poście
zadanie rozbijmy na dwa przypadki:
1) wielokąt ten posiada parzystą liczbę boków
2) posiada nieparzysta liczbę boków
(1) (rysunek dla 6 boków)
zauważasz, że w wielokącie foremnym o parzystej liczbie boków ... każdemu bokowi odpowiada
dokładnie jeden bok tej samej długości, równoległy do niego ... a więc odległość punktu
(leżącego pomiędzy nimi lub ich przedłużeniami) od obu tych boków będzie stala i będzie
wynosić dokładnie tyle ile wynosi odległośc pomiędzy tymi dwoma bokami
(2) w następnym poście
 To "część" tego wielokąta
To "część" tego wielokąta
 Ale co w przypadku jeżeli punkt będzie tutaj?
Ale co w przypadku jeżeli punkt będzie tutaj?
