.
Dżerzi: Rozwiąż nierówność IxI/x − I2x−6I < 5x + 1
Bardzo proszę od dokładne rozpisanie zadania

3 kwi 12:16
Kaja: | | ⎧ | x, dla x>0 | |
| |x|= | ⎩ | −x, dla x<0 |
|
| | ⎧ | 2x−6, dla x≥3 | |
| |2x−6|= | ⎩ | −2x+6, dla x<3 |
|
1. x∊(−
∞, 0)
−1+2x−6<5x+1
3x>−8
x>−
83 i x∊(−
∞,0)
zatem x∊(−
83,0)
2. x∊(0,3)
1+2x−6<5x+1
3x>−6
x>−2 i x∊(0,3)
zatem x∊(0,3)
3. x∊<3,+
∞)
1−2x+6<5x+1
7x>6
x>
67 i x∊<3,+
∞)
zatem x∊<3, +
∞)
odp. x∊(−
83,0)∪(0,+
∞)
3 kwi 12:26
Dżerzi: Kaja , nie rozumiem właśnie dla czego 1 przedział jest od −& do 0 ,
wiem że to ma wynikać z definicji bezwzględności
ale jak jest ten ułamek IxI/x to dlaczego właśnie ten przedział a nie na przykład od 0 do + &

3 kwi 12:31
Dżerzi: już wiem bo dla całej tej nierówności wyznaczamy przedziały od lewej do prawej czyli od
+ do − , tak

bo dalsze dwa to wiem <0,3) <3,+&) tak aby x−sy się nie zerowały
3 kwi 12:33
Kaja: narysuj sobie oś i zaznacz punkty 0 i 3. te punkty podzieliły os właśnie na trzy przedziały
3 kwi 12:36
Dżerzi: okey, a jeszcze jedno pytanie , jak liczysz x dla przedziału
(0,3) i wychodzi ci x>−2 to to dla czego
rozwiązaniem jest xe(0,3) a nie część wspólna przedziału
(0,3) i (−2,+&)

3 kwi 12:41
krystek: A co jest cz wspólną − iloczynem tych przedziałów?
3 kwi 12:44
Kaja: a jaka jest część wspólna tego przedziału? nie (0,3) ?
3 kwi 12:45
krystek: Oczywiście! to było do@Dżerzi
3 kwi 12:46
krystek:
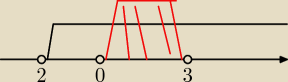
3 kwi 12:48
Dżerzi: tak macie rację , narysowałem sobie ośkę i zrozumiałem ,
dzięki wam za pomoc a szczególnie Kaji za obfite rozrysowanie zadania pozdrawiam

3 kwi 12:48
Kaja: cieszę się , że pomogłam

3 kwi 12:52


 bo dalsze dwa to wiem <0,3) <3,+&) tak aby x−sy się nie zerowały
bo dalsze dwa to wiem <0,3) <3,+&) tak aby x−sy się nie zerowały



