ciąg liczbowy mala2: Zbadaj monotoniczność ciągu a_n=(3−n)². −−−−−− Obliczyłam a_n+1=(2−n)² a_n+1−a_n=−2n+5 Nie wiem, czy to jest >, < od zera. i "na piechotę' ciąg:4, 1, 0, 1, 4 Nie wiem jak odpowiedzieć. Proszę o pomoc. Wychodzą mi przedziały. ?

Tomek: mi wyszło trochę inaczej 2n+5 n należy do naturalnych wiec kazda liczba 2n+5 > 0 wiec ciąg rosnący według mnie tak powinno być...

Technik: a_n+1 [3−(n+1)]² =(2−n)²=4−4n+n² a_n+1−a_n=n²+4−4n−(3−n)²= n²+4−4n−(9−6n+n²)= n²−4n+4−9+6n−n²= 2n−5 ciąg jest malejący

Technik: a no tak ciąg jest rosnący przepraszam bo n∊N₊

Aga: tam Ci wychodzi nie −2n+5 tylko 4n−5 z tego wynika, że ciąg nie jest monotoniczny to nie wystarczy?

Aga: a, sorki, 2n−5

Dominik: a wg mnie ciag maleje w przedziale <1, 3) oraz rosnie w (3, ∞)

Tomek: wyszła funkcja liniowa wiec ciąg musi byc albo rosnący albo malejący ale skoro współczynnik przy n jest dodatni to ciąg jest rosnący i mój błąd powinno byc 2n−5

zombi: Skoro różnica wyrazów jest zależna od n to jest to ciąg nie monotoniczny

Tomek: zombi masz racje jezeli chodziłoby o ciąg arytmetyczny bo wtedy obliczamy tak różnice ale w zadaniu nic nie jest napisane czy jest to ciąg arytmetyczy. tak sądze

Dominik: sugerujecie ze funkcja kwadratowa (3 − n)² z dziedzina n∊ℕ₊ nie jest monotoniczna? BZDURY maleje i rosnie w okreslonych przedzialach.

Tomek: ja sądze ze jest tylko rozsnąca bo różnica wychodzi 2n−5 a więc dla kazdego większego n warość również rośnie

zombi: http://pl.wikibooks.org/wiki/Matematyka_dla_liceum/Ci%C4%85gi_liczbowe/Monotoniczno%C5%9B%C4%87_ci%C4%85gu Nasz ciąg w jednym przypadku rośnie a drugim maleje, więc jest nie monotoniczny, gdyby pytali o przedziały monotoniczności to wtedy można podawać gdzie jaki. Przykłady z kiełbasy n²−9n−5 jest nie monotoniczny bo dla niektórych n jest malejący a dla niektórych rosnący.

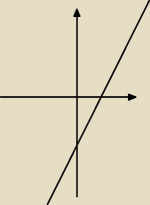
Tomek: ale ty podałeś funkcje kwadratową to wiadomo ze rosnie i maleje ale 2n−5 nie jest funkcją kwadratową tylko liniową a taka funkcja albo maleje albo rosnie nie ma innej opcji ( jeszcze moze byc stała ale mamy 2n) to jest nasza funkcja

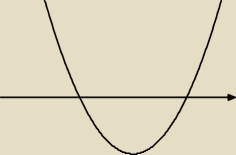
Tomek: a to jest twoja chyba jest różnica

krystek: badamy różnice jak a_n+1−a_n=(3−(n+1))²−(3−n)²=(2−n)²−(3−n)²=4−4n+n²−9+6n−n²=2n−5 jest to ujemne dla n=1,2 a dla n>2 dodatnie więc jest przedziałami rosnacy i malejacy

zombi: A ona jaki ciąg podała? Też kwadratową.

Dominik: dobra, zwracam honor. gdzie nie spojrze to monotonicznosc jest definiowana dla calej dziedziny, ciag nie moze rosnac czy malec przedzialami. zatem jest niemonotoniczny.

mala2: Rozumiem Bardzo dziękuję.