geometria płaska aneta: 1. W trójkącie prostokątnym ABC stosunek przyprostokątnych jest równy AB:AC=4:3. Punkt D dzieli przyprostokątną AB na odcinki takie że DB=3AD. Punkt E należy do przeciwprostokątnej BC i odcinek DE jest prostopadły do boku BC. Oblicz jakim procentem pola trójkąta trójkąta ABC jest pole trójkąta DBE. 2. W trójkącie ostrokątnym równoramiennym ABC, AC=BC, poprowadzono wysokości CD i BE. Pole trójkąta ABE jest o 44% większe od pola trójkąta ADC. Wiedząc, że obwód trójkąta ABC jest równy 80cm, oblicz pole trójkąta ABC. Proszę pomóżcie rozwiązać te zadania, bo nie mam pojęcia jak je ruszyć

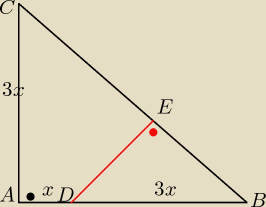
irena_1: 1. |AB|=4x

	1
|AD|=		|AB|=x
	4

|BD|=3x |BC|²=(3x)²+(4x)²=25x² |BC|=5x Trójkąty DEB i ABC są podobne. s− skala podobieństwa DEB do ABC

	3x		3
s=		=
	5x		5

Stosunek pól jest równy kwadratowi skali podobieństwa

PDEB		9
	=s2=		=36%
PABC		25

P_DEB=36%P_ABC

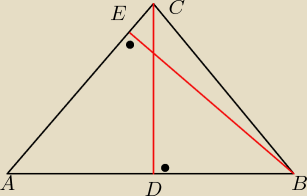
irena_1: 2. Trójkąty ABE i ACD są podobne s− skala podobieństwa trójkąta ABE do ACD s²=144%=1,44 s=1,2

	|AB|
s=
	|AC|

|AB|=1,2|AC| 1,2|AC|+2|AC|=80 3,2|AC|=80 |AC|=25cm |AB|=1,2*25=30cm |CD|²+|AD|²=|AC|² |CD|²=25²−15²=625−225=400 |CD|=20cm

	1
PABC=		*30*20=300cm2
	2