Wpisujemy walec kuleczka: W półkulę o promieniu R wpisano walec, którego przekrojem osiowym jest kwadrat. Oblicz długość promienia i wysokość tego walca. Jakieś wskazówki?

az: Podaj odpowiedź, jeśli możesz.

kuleczka: Niestety nie ma odpowiedzi..

az: rys

kuleczka: Mam pytanie: czy jeśli w zadaniu nie podali a jako danej to mogę się nią posługiwać?

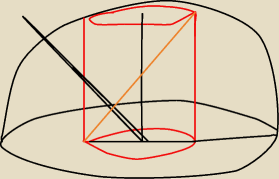
rafal: promień półkuli to R Wysokość walca to H średnica okręgu w postawie walca to też H, ponieważ przekrój osiowy jest kwadratem. promień walca to 1/2 H. suma promienia półkuli i promienia walca zatem, to R+1/2 H oznaczamy kąt między przekatną przekroju osiowego walca (linia pomarańczowa) linia czarną w postawie (R+1/2H) jako α zapisujemy: tgα=^H_R+1/2H z tego otrzymujemy wysokość walca: H=tgα(R+1/2H) długośc promienia tego walca to połowa średnicy jego podstawy więc otrzymany wyżej wynika dzielimy na 2 i otrzymujemy: r=^tgα(R+1/2H)₂ powinno być dobrze

kuleczka: Ok, cofam.. Przedstawiam a jako pochodną R poprostu.. Dzięki!

rafal: sorry za rysunek xD ale walczyłem żeby coś takiego nawet uzyskac