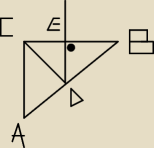
 Środkowa kąta przy wierzchołku C w trójkącie ABC przecina bok AB w punkcie D. Półprosta DE jest
dwusieczną kąta BDC. Wykaż że jeżeli DE jest prostopadłe do BC to trójkąt ABC jest
prostokątny,
Środkowa kąta przy wierzchołku C w trójkącie ABC przecina bok AB w punkcie D. Półprosta DE jest
dwusieczną kąta BDC. Wykaż że jeżeli DE jest prostopadłe do BC to trójkąt ABC jest
prostokątny,
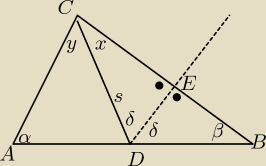 Zał.
AD=DB
DE→ dwusieczna
T.
∡ACB=900 ⇔ΔACB jest prostokątny.
D.
W ΔDBE:
δ+β=900
W ΔDEC:
δ+x=90⇔x=β⇔ΔCDB i ΔCDA − Δrównoramienne
y=α
W Δ ABC:
2α+2β=180⇔α+β=90⇔
∡ACB=900 ⇔ΔACB jest prostokątny.
Zał.
AD=DB
DE→ dwusieczna
T.
∡ACB=900 ⇔ΔACB jest prostokątny.
D.
W ΔDBE:
δ+β=900
W ΔDEC:
δ+x=90⇔x=β⇔ΔCDB i ΔCDA − Δrównoramienne
y=α
W Δ ABC:
2α+2β=180⇔α+β=90⇔
∡ACB=900 ⇔ΔACB jest prostokątny.