Gdyby nie 1
Licealista_Theosh: Największa i najmniejsza watrość funkcji kwadratowej.
Oblicz dla jakiego argumentu funkcja przyjmuje największą a dla którego najmniejszą.
Gdyby nie ta 1 w liczniku nie byłoby problemu
2 kwi 20:47
Aga: spoko, spoko, czekaj, już się robi xD
2 kwi 20:48
Skipper:
... a tak ... jaki problem ?−
2 kwi 20:49
Licealista_Theosh:
| | 1 | |
Z tą 1 w liczniku. W odpowiedziach jest największa |
| a najmniejsza 18
|
| | 4 | |
@Aga nie musisz mi robić, tylko wytłumacz jak zrobić
2 kwi 20:51
Licealista_Theosh: Pokierujecie chociaż?
2 kwi 20:54
Skipper: to może przepisz porządnie to zadanie−
2 kwi 20:57
Aga: a więc tak, ta jedynka nic nie utrudnia
, żeby funkcja przyjęła najmniejszą wartość to tak
na logikę mianownik musi być jak największy, a żeby przyjęła jak najmniejszą wartość to
mianownik musi być jak najmniejszy.
Najpierw jak zawsze DZIEDZINA xD ... x należy do R bo delta jest ujemna.
Teraz tak, mianownik nie nie ma maksimum bo a>0 (a=1). Więc Funkcja nie przyjmuje największej
wartości.
Teraz liczymy minimum mianownika:
Δ=16−32=−16
minimalna wartość to q=−Δ/4a czyli
q= 16/4=4.
więc cała funkcja to będzie f(x) = 1/4 − wartość maksymalna
...minimalnej nie przyjmuje xD
2 kwi 20:58
Skipper:
pewnie ma jakiś przedział−
2 kwi 21:00
Licealista_Theosh: No fakt trochę źle przepisałem.
Wyznacz wartość największą i najmniejszą funkcji f w podanym przedziale
Obliczyłem deltę i wychodzi
Δ= 16−32= −16
I podstawiam za x
| | 1 | |
I wychodzi |
| czyli wartość największa Dopiero teraz wpadłem a jak obliczyć najmnieszą? |
| | 4 | |
2 kwi 21:01
Licealista_Theosh: Dzięki @ Aga. Zmarnowałem twój czas, bo dopiero teraz się zorientowałem że mam podstawić
Tylko jak obliczyć wartość najmniejszą ?
2 kwi 21:02
Aga: najmniejszą, to musisz poszukać największej wartości licznika czyli kiedy x
2 − 4x + 8
przyjmuje max. w Twoim przedziale
2 kwi 21:07
Licealista_Theosh: ?
2 kwi 21:07
Licealista_Theosh: A jak to się robi? Wybieram po kolei argumenty i liczę?
2 kwi 21:08
Aga: x
2 −4x + 8 ma wierzchołek w x=2 więc max wartość będzie w punkcie najbardziej odległym od 2
czyli w przypadku tego przedziału w x=4
2 kwi 21:10
Licealista_Theosh: aha.
2 kwi 21:10
Licealista_Theosh: Dzięki.
2 kwi 21:10
Aga: więc jak już masz to x=4 to podstawiasz to mianownika i mianownik wychodzi 16−16+8 = 8 czyli
f(x)=1/8
2 kwi 21:11
Skipper:
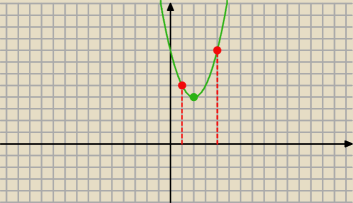
... to jest Twój mianownik−
2 kwi 21:11
Aga: nmzc
2 kwi 21:11