Jak się za to zabrać wogóle?
P-rzemek: Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 6, a krawędź boczna − 4. Oblicz
cosinus kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny jego podstawy.
2 kwi 20:14
pigor: ... , otóż, niech h
b − wysokość ściany bocznej, a H − wysokość ostrosłupa,
to
H2= 4
2−(
23*
12*6
√3)
2=16−4*3=
4, więc
h
2b= H
2+(
13*
12*6
√6)
2= 4+6=10 ⇒
hb=√10 , zatem
jeśli α − kąt dwuścienny ściany bocznej z podstawą, to jego miarą
jest kąt liniowy między wysokością podstawy i h
b ściany bocznej,
czyli
| | 13*12*6√3 | | √3 | |
cos α= |
| = |
| = √0,3 = 0,1 √30. ...  |
| | √10 | | √10 | |
2 kwi 20:40
Aga: A ile ma wyjść?
√21 / 7 ?

2 kwi 20:41
pigor: ..., O

. ...

, coś u mnie nie tak

2 kwi 20:43
Aga: A więc, jak sobie to narysujesz, to zobaczysz że cosinus szukanego kąta to jest stosunek 1/3
długości wysokości podstawy do wysokości ściany bocznej

wysokość podstawy to 6
√3 / 2
czyli 3
√3. Z tego 1/3 czyli
√3. Liczymy wysokość ściany bocznej (z pitagorasa) i
wychodzi
√7. Szukany cosinus to
√3 /
√7 − po usunięciu niewymierności z mianownika
√21 / 7

2 kwi 20:45
Aga: wysokość ściany bocznej troszkę nie tak

2 kwi 20:46
pigor: ...ach

, jest błąd przy H
b 6 zamiast 3),
| | √3 | |
a więc: h2b= 4+3=7 ⇒ hb=√7 ⇒ cos α= |
| = 17√21 . ...  |
| | √7 | |
2 kwi 20:48
dero2005:
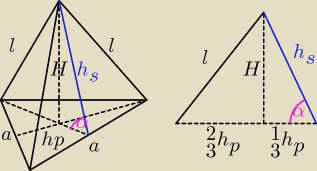
h
p − wysokość podstawy
H =
√l2 − (23hp)2 =
√42 − (233√3)2 =
√16 − 12 =
√4 = 2
h
s =
√H2 + (13hp)2 =
√22 + (13*3√3)2 =
√4 + 3 =
√7
| | 13hp | | 13*3√3 | | √21 | |
cos α = |
| = |
| = |
| |
| | hs | | √7 | | 7 | |
2 kwi 20:49
pigor: ... , oczywiście błąd przy liczeniu nie H
b , tylko h
b . ...

2 kwi 20:49
P-rzemek: Ma wyjść √21 / 7 czyli się aligancko zgadza, wielkie dzięki za pomoc

2 kwi 21:29


 . ...
. ...  , coś u mnie nie tak
, coś u mnie nie tak 
 wysokość podstawy to 6 √3 / 2
czyli 3 √3. Z tego 1/3 czyli √3. Liczymy wysokość ściany bocznej (z pitagorasa) i
wychodzi √7. Szukany cosinus to √3 / √7 − po usunięciu niewymierności z mianownika
√21 / 7
wysokość podstawy to 6 √3 / 2
czyli 3 √3. Z tego 1/3 czyli √3. Liczymy wysokość ściany bocznej (z pitagorasa) i
wychodzi √7. Szukany cosinus to √3 / √7 − po usunięciu niewymierności z mianownika
√21 / 7 

 , jest błąd przy Hb 6 zamiast 3),
, jest błąd przy Hb 6 zamiast 3),

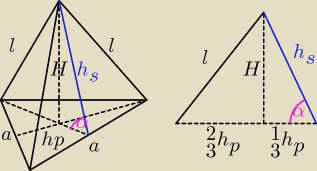 hp − wysokość podstawy
hp − wysokość podstawy

