"Równania kwadratowe z parametrem" BR: Proszę o pomoc w zadaniu: Zbadaj liczbę rozwiązań równania ze względu na wartość parametru m (m ∊ R). Napisz wzór i narysuj wykres funkcji y=g(m), która każdej wartości parametru m przyporządkowuje liczbę rozwiązań równania: a) (m−5)x²−4mx+m−2=0 Jakby ktoś mógl w pktach zapisać jak to się rozwiązuje..

Bogdan: (m−5)x² − 4mx + m − 2 = 0 a = m − 5, b = −4m, c = m − 2 Dla a = 0: m − 5 = 0 ⇒ m = 5 ⇒ −20x + 3 = 0, jest jedno rozwiązanie. Dla a ≠ 0: m − 5 ≠ 0 ⇒ m ≠ 5 Badamy znak Δ.

	10
Δ = 16m2 − 4(m − 5)(m − 2) = 12m2 + 28m − 40 = 12(m +		)(m − 1)
	3

	10
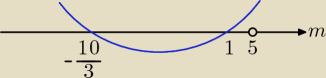
Są dwa rozwiązania dla Δ > 0: m∊(−∞, −		)∪(1, 5)∪(5, +∞)
	3

	10
Jest jedno rozwiązanie dla Δ = 0: m∊{−		, 1}
	3

	10
Nie ma rozwiązań dla m∊(−		, 1)
	3

Odp.:

	10
Są dwa rozwiązania dla Δ > 0: m∊(−∞, −		)∪(1, 5)∪(5, +∞),
	3

	10
jest jedno rozwiązanie dla Δ = 0: m∊{−		, 1, 5},
	3

	10
nie ma rozwiązań dla m∊(−		, 1)
	3

Za chwilę pokażę wykres y = g(m).

Bogdan: Wykres funkcji y = g(m) zaznaczyłem kolorem czerwonym