okrąg zosia.mat: Wyznacz współrzędne środka okręgu opisanego na trójkącie o wierzchołkach A(−2,0), B(6,0), C(4,6)

Janek191: ( x − a)² + ( y − b)² = r² ===================== A = ( − 2; 0) B = ( 6; 0) C = (4; 6) więc po podstawieniu otrzymamy : ( − 2 − a)² + ( 0 − b)² = r² ( 6 − a)² + ( 0 − b)² = r² ( 4 − a)² + ( 6 − b)² = r² czyli 1) 4 + 4 a + a² + b² = r² 2) 36 − 12 a + a² + b² = r² 3) 16 − 8 a + a² + 36 − 12 b + b² = r² Od 2) odejmuję 1) 32 − 16 a = 0 ⇒ 16 a = 32 ⇒ a = 2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Wstawiam 2 za a do 1) i do 3) 4 + 8 + 4 + b² = r² 16 − 16 + 4 + 36 − 12 b + b² = r² Otrzymuję 16 + b² = r² 40 − 12 b + b² = r² Wykonuje odejmowanie ( 40 − 12 b + b²) − ( 16 + b²) = r² − r² 24 − 12 b = 0 ⇒ 12 b = 24 ⇒ b = 2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Odp. S = ( a; b) = ( 2; 2) ================

pigor: ..., lub np. tak : środek okręgu opisanego na Δ, to punkt przecięcia sie symetralnych, więc np. s_AB : środek AB, to D=(2,0) i AB^→=[8,0] ⇒ ⇒ 6x+C=0 i 6*2+C=0 ⇒ 6x−12=0 ⇔ x=2 − równanie s_AB − symetralnej boku AB ; s_AC : środek AC, to E=(1,3) i AC^→= [6,6]=6[1,1] ⇒ ⇒ x+y+C=0 i 1+3+C=0 ⇒ C=−4 i x+y−4=0 − równanie symetralnej s_AC boku AC, zatem x=2 i 2+y−4=0 ⇒ x=2 i y=2 , czyli (a,b)= (2,2) − szukane współrzędne środka okręgu opisanego na danym Δ. ...

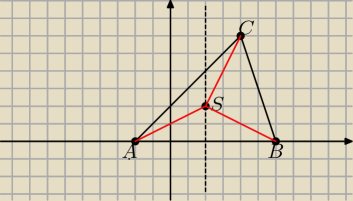
Aga1.: s_AB: x=2 Środek okręgu leży na symetralnej boku AB , więc S(2,y) i ponadto ISAI=ISCI=ISBI=r. √16+y²=√4+(6−y)² /² 16+y²=4+y²−12y+36 y=2