umca Kipic: Ze zbioru liczb {1,2,3,4,5,6,7,8}wybieramy losowo jednoczesnie cztery liczby . Oblicz prawdopodobienstwo zdarzenia A polegajacego na tym z najmnijesza wylosowana liczba bedzie 3 lub najwieksza wylosowana liczba bedzie 7 A₁ zdarzenie poegajace na tym ze najmniejsza wylosowana liczba jest 3 wiec

	5 3
A1=

dlaczego tak skad sie bierze 5 czy aby z tego ze dla drugiego zdarzenia ze najwikssza jest 7

	5 3
to juz jedno miejsce musi byc zajete i niema . A to 3 z		to chodzi o to ze cyfry 1 2 3

to tak jakby 1 ?

PuRXUTM:

	5
dzisiaj pisałem próbną z tym zadaniem w szkole wyszło mi chyba		ale nie jestem pewny
	7

na 100%

Kipic:

27
	jakbys wczoraj siedzial do 00:00 to uzytkownik @matura ktory ma przecieki i pewniaki
70

z matury rozszerzonej to w tym arkuszu co podal bylo wlasnie to zadanie i jakbys zrobilmialbys dobrze

Kipic: a wogule dzisiaj sie szlo do szkoly

use: masz zbiór {1,2,3,4,5,6,7,8} razem 8 liczb wybieramy 4 ale najmniejsza wylosowana ma byc 3 lub największa bedzie 7 wiec zeby najmniejsza byla 3 to losuje z 6 4 czyli 6 po 4 i druga mozliwosc najwieksza ma byc 7 czyli 7 po 4

	5
i dzieląc to przez Ω wyjdzie		czyli tak jak Purxutumowi
	7

PuRXUTM: ale to była jakaś matura krajowa że ma przecieki, ja byłem w szkole ale inni nie byli

	27		6 4		7 4
ale dlaczego		ja mam że moc A =		+
	70

PuRXUTM: a reszte macie odpowiedzi bo bym sobie sprawdził

use: tez mi tak wyszlo spojnik lub sugeruje sume dwóch przypadków

Kipic: zle macie zle rozumujecie to zadanie macie tutaj http://pliki.pomorska.pl.s3.amazonaws.com/dokumenty/Przyk%C5%82adowe%20rozwi%C4%85zania_PR_Matematyka_2013_1.pdf 9 zadanie i tyle w tym temacie moze mi ktos wytllumaczyc skad sie to bierze w moim 1 poscie

use: ogolnie to prawdopodobienstwo jest masakryczne czasami

Kipic: no wlasnie use mi jescze inaczej wyszlo traktowalem najpier 3 jako jedno a pote 7 jako jedno i

	33
wyszlo mi chyba najblizej wtedy bo		a skad w odpowiedziaxhc jest to to niemam pojecia
	70

use: wiemjuz widze swoj błąd ... musze zapewnic liuczbe 3 w losowaniu a w moim przypadku moze byc tak ze w ogole wsrod wylosowanych nie bedzie liczby 3 ^^

use: jezeli zapewniam liczbe 3 topzostaje mi kombinacja liczb {4,5,6,7,8} czyli 5 po 3 , analogiocznie dla siódemki

PuRXUTM: czyli kicha...

use: kicha ^^ lepiej teraz wyciągnąc wnioski niz po maturze ^^

PuRXUTM: a jeszcze pytanie czy równoległobok jest trapezem równoramiennym

use: raczej tak

use: trapezem to chyba jest wszystko xd

Kipic: mo jasne ze o to chodzi tylko ze tych zadan jest tak duzo roznych ze to zadanie jest malo istotne

Kipic: no jest

Kipic: na 100%

use: 79% juz

PuRXUTM: ja uznałem że nie więc kolejna kicha, bo sobie pomyślałem że trapez równoramienny przy podstawach ma kąty o takiej samej mierze a tutaj nie, w ogóle strasznie to spaściłem, choć po napisaniu myślałem że jest ok....

Kipic: jakby w maju dali chociaz troche z tego arkusza to by bylo git http://pliki.pomorska.pl.s3.amazonaws.com/dokumenty/Matematyka_arkuszPR_2013.pdf

use: http://www.youtube.com/watch?v=85OeQEW4sHg widzieliscie to może

Kipic: wczoraj to ogladalem hardcorowe to jest zwlaszcza ten montaz piosenek w polaczeniu z emocjami

use: najlepsze jest to : O nie! Tylko nie całka potrójna dziewiątego stopnia z logarytmu naturalnego granicy sinusa z pierwiastka sześciennego po obszarze omega!

Kipic: ale to jest tez swietne za kazdym razem gdy slucham to mnie dobija hehe http://www.youtube.com/watch?v=qIZt2NdP_08

use: http://www.sendspace.com/file/ak9yk2 link do podkowy

PuRXUTM: na ile byś to napisał use, kipic ? ja myślę będzie pewnie 60%... spaściłem

Kipic: ja jak to dzisiaj rano wydrukowalem i zrobilem to tak na okolo 50 moze wiecej ale krotko to robilem nawet nie 1 godzine

Kipic: a sa 3 godziny

use: ja jak pisze to zawsze te 50% minimum mam ( zależy jak pytania ) ale jak wdomu pisałem kilkanascie arkuszy po 2,5 h to liczyłem tylko zadania w pełni rozwiązane bez błędu i miałęm zawsze te 50% wiec myśle że jak dobrze pujdzie to może nawet bedzie ponad 80% , ciężko powiedzieć

Mati : pomożecie prosze ? ? ? jak to rozwiązac : 3x5−6x3=0 oraz : I3x−9I≥15

use: sciąga się wam ta podkowa ?

use: 3x−9≥15 V 3x−9≤15

use: w drugim minus 15 −15

Kipic: no wie @ mati tak : l3x−9l≥15 to masz : 3x−9≥15 i 3x−9≤−15 i rozwiazujesz i odpowiedz koncowa to suma tych 2 przedzialow a 3x⁵−6x³=0 to 3x³(x²−2)=0 wiec x=0 i x²−2=0 ⇒x²=2 ⇒ x=√2 i x=−√2

Technik: kipic fizyka się ładuje już

use: Kipic sciaga sie ta podkowa czy nie >>

Kipic: Siemka @Technik chcesz to moge ci tutaj napisac hardcorowe zadanko z fizy z rozszerzenia jesli chcesz ozywiscie bo jak robilem to mnie rozwalilo nawet nie wiedzialem jak tknac

Kipic: tak use pobiera sie

Ksenia : a jak rozwiazać ten ukłąd rówan ⎧ x−2y4=−2 ⎩ 6x−2y=4

use: to ok chcialem sie upewnic czy dobrze sie dodało

Technik: napiszesz mi na e−mail to zadanie a najlepiej fotkę ja się teraz gimnastykuje nad matematyką z fizyki to oczywiście pierwsza część 261 zadań jutro wyśle dwa razy tyle

use: co znaczy −2y4 ?

Ksenia : to ma być układ równań w klamrze ^x−2y₄=−2 6x−2y+4

Technik: to co za problem masz ? prosty układ równań a gdzie w drugim jest =

Kipic: o w jape a ja rozwiazuje z ze to x−2y⁴=−2 ale cos mi nie wyszedl zaden pierwiastek tylko y = 0 ale jesli to jest podzielone przez 4 to zmienai postac rzeczy

Ksenia : * 6x−2y=4

Technik:

x−2y
	=−2
4

6x−2y=4 −2y=4−6x / (−1) 2y=−4+6x/2 y=3x−2 wstawiasz do pierwszego

x−2(3x−2)
	=−2 i licz
4

Mila:

	8 4
Ω=		=70

A₃− najmniejsza wylosowana liczba to 3 zdarzenia sprzyjające: (3,xxx) pozostałe 3 liczby losujemy ze zbioru{4,5,6,7,8} mamy :

5 3
	=10 możliwości

A₇− największa wylosowana liczba to 7 (xxx7) pozostałe 3 liczby losujemy ze zbioru:{1,2,3,4,5,6} mamy:

6 3
	=20 możliwości

Musimy odjąć pewne zdarzenia, gdy w A₃ jest 7 i w A₇ jest 3 ( wśród 4 liczb "3" jest najmniejsza i "7" największa, ) (3xx7) dwie pozostałe liczby ze zbioru {4,5,6} mamy:

3 2
	=3

	10+20−3
P(A3)+P(A7)−P(A3∩A7)=
	70

use: ja patrzylem jak na AGH się progi punktowe układają to jest szok generalnie na kazddy lepszy kierunek prog jest minimum 600pkt ( tak bylo w ubieglych latach ) mozna maks miec 1000 pkt za angielski 1pkt=1% z podstawy z rozszerzenia 2pkt=1% maks 200 pkt za jezyk i za matme jest tak ze G= N+2 * (N−30 ) dla 30% ≤ N ≤ 80% z rozszerzenia gdzie N to procenty lub G=N+100 dla N>80% i ostateczny wzor na punkty to W=4 * G +J ( jezyk ) czyli piszac matme na 60% G=120 przyjmiemy jezyk na 40% czyli 40 pkt wiec W=4*120+40=520 masakra przydałoby się wiec te 85 % z matmy mieć ^^

Kipic: wiec 1 rownanie mnozysz *4 wiec wychodzi x−2y=−8 x−2y=−8 6x−2y=4 z 1 wyznaczasz x wiec x=2y−8 podstawiasz do 2 rownania 6(2y−8)−2y=4 12y−48−2y=4 10y=52

	52
y=
	10

podstawiamy

	52
x−2(		)=−8
	10

	80		104
x=−		+
	10		10

	24
x=
	10

Kipic: Mila jak zwykle swietnie wytlumaczone dziękuję

use: Kipic stukasz jakis arkusz z tej podkowy potem sie pochwalisz ile % tylko tak szczerze

PuRXUTM: Mila jak oceniasz ten arkusz, może być podobny w maju

Kipic: @use o kurcze sporo tego

Kipic: @use jak moge stukac jak caly czas tu pisze i analizuje ten co wyzej podalem

Technik: @use tam też jest podstawa bo nie wiem czy ściągać to

use: tylko rozszerzenie

Kipic: @Technik specjalnie dla Ciebie zrobione zdjęcie i wrzucone na serwer tutaj masz link http://www.sendspace.com/file/duubw8 Hardcorowe to zadanko

Technik: Kipic UWAGA: onet.pl nie przyjmie Twojej wiadomości. Załączniki przekraczają 36,0MB

Technik: zobacz pocztę

Kipic: Dobra @use zaczynam robic ten 1 arkusz ze strony 235

Mila: Podaj, Kipic linka do arkusza, przeanalizuję i odpowiem.

use: ja tez go zaczynam wlasnie to do dzieła

Kipic: @Technik dostalem te wszystkie zdjecia

use: tylko nie oszukuj ^^

Kipic: Prosze @Mila jesli chodzi o ten hardcorowy to masz tutaj : http://pliki.pomorska.pl.s3.amazonaws.com/dokumenty/Matematyka_arkuszPR_2013.pdf

Technik: @Kipic zadanie nie jest takie trudne jak się wydaję

Kipic: @use nigdy nie oszukuje zreszta oszukiwanie kogos tak naprawde polega na oszukiwaniu samego siebie wiec sie nie oplaca

use: Kipic potem pogadamy ktore sprawiły problem zadania z tego arkusza ok

PuRXUTM: Mila jak oceniasz tą maturę ?

Kipic: @Technik moze dla Ciebie bo dla mnie to przepasc

use: dobra zaczynam pisac ^^

Kipic: @use dobra to do dziela biore sie teraz za ten wlasnie 1 arkusz ze strony 235

Technik: @Kipic doszło na pocztę

Kipic: tak mam to

Kipic: dzięki

Technik: @Kipic i jak mogą być czy trudniejsze chcesz

Kipic: @Technik ja jestem narazie lamerem z fizy a teraz robie arkusz 1 wiec za bardzo przestalem myslec o energiach hehe ale jak ogarne je to napisze

Technik: mam takie zadanko z matmy pomożesz

Kipic: @Technik to dawaj moze bede wiedziec a czas mi ucieka ze 180 minut ktore mam na arkusz juz 16 minut go robie a ze mam wlaczony monitor i odswiezanie strony to widze czy ktos tu cos wkleja

Technik:

	a1		a2
wykaż że jeśli		=		i b1+b2+.......+bN≠0 to
	b1		b2

	a1+a2+....+aN		a1
		=		na tym zadaniu właśnie skończyłem swoja
	b1+b2+.....+bn		b1

przygodę z maturą roz

Kipic: @Technik takie zadania zaczynaja mnie przesladowac wlasnie ich nigdy nie robilem bo postanowilem ze szanse trafienia w takie zadanie niczym ciag ze zbiorami na liczbach to marne szanse akurat w tego typu zadaniach nie potrafie Tobie pomóc wogule liczby rzeczywiste i ciagi sobie odpuscilem z rozszerzenia , wedlug mnie to strata czasu a zazwyczaj jest jedno zadanie na maturze

Kipic: A ktos wie

use:

	a1		a2
jezeli		=		⇒a2=x*a1 i b2 = x*b2 x∊R
	b1		b2

b1+b2+.......+bN≠0 czyli nie ma dzielenia przez zero zatem

a1+x*a1+...+y*a1		a1
	=
b1+x*b1+....+y*b1		b1

use: y∊R

use: wydaje mi sie ze to jest ok bo jak dodamy x+y tych a1 i x+y tych b1 to si skróci i zostanie a1/b1

Technik: skąd tam wziął się x

use:

	1
podstawiłem go swiadomie bo zobacz jak masz		={2}{4} to 2 = x *1 czyli a2 = x * a1
	2

use:

1		2
	=		⇒ to 2 = x *1 czyli a2 = x * a1
2		4

use: albo 1 = x * 2

Technik: nadal nic z tego nie kumam @use miałeś próbny egzamin zawodowy

use: chłopie ja mam taką szkołe że pisaliśmy btych egzaminów już 7 ( za kazde dostawalismy ocene na dopa 75 % tyle co na egzaminie ) ^^

Technik:

use: technik zobacz jak mam a1+x*a1+....+y * a1 i tyle samo mam w mianowniku liczb b1 to jak to dodam to mam (x+y)a1 / (x+y)b1 czyli sie to skróci wiec = a1/b1 ( musisz sobie to wyobrazic bo akurat nie ma liczb ale wyobraz sobie ze a1 i b1 to liczy oraz x i y tez liczby

Technik: ok

Kipic: w okolo 1h i 15 minut udalo mi sie wmiare dobrze zrobic 1, 2, 4, 6, 7(w polowie), 8 i

	3
10(tak		) a z reszta to tak po 1−2 punkcie jedynie nie tknalem 9 bez pomyslu na to
	4

zadanie

Kipic: czyli tak mysle ze by byla polowa gdyby to sprawdzali na komisji

Mila: Spokojnie Panowie, nie mogę się połączyć ze stroną.

use: http://www.youtube.com/watch?v=9cTsf4W2JZQ

use: ja zrobilem bezbłędnie 1,2,3,4 poki co teraz sie zawiesilem na 5 ^^

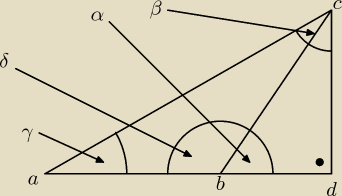
Kipic: najsmieszniejsze jest zadanie 4 bo skoro mamy tyle danych <RYSUNEK> to wiemy z opisu ze trojkaty ABC i BDC sa rownoramienne wiec w trojkacie BDC mamy katy 45 stopni i jeden prosty 90 stopni wiec mozna policzyc δ =180−45=105 wiec wiemy takze ze ABC jest rownoramienny wiec γ =22,5

	1
wiec kat β = 67,5 a to jest okolo 0,39 wiec 0,39<		lol smieszne zadanie wsumie nic innego
	2

nie trzeab robic i powinni to uznac

Mila: Na razie udało mi się ściągnąć arkusz podstawowy i uważam, że wcale nie jest taki łatwy. Można zrobić sporo błędów w zamkniętych, a otwarte są pracochłonne. Radzę Wam , abyście dobrze przejrzeli ten arkusz i zrobili od a do z.

use: ja lioczyłem normalnie na bokach i mi wyszedł ulamek z pierwiastkiem kalkulator licxzy ze jest rowny 0,3826834... zle zaokrągliles

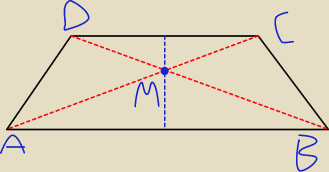
use: mnie zastanawia inna rzecz mam trapez : PΔABM =25 PΔDCM=16 nie nwiem czy jest on równoramienny nic w tresci nie ma to na jakiej podstawie ΔABM~ΔDCM ?>

use: H=18 trzeba policzyc pole trapezu

Kipic: @use na bokach tez mozna ale drugi sposob ten co pokazalem wydaje mi sie lepszy o wiele szybciej mozna to zrobic niz bawic sie na bokach ale bokami zrobilem zeby sie nie przyczepili oczywiscie on nie jest rownoramienny ja jedynie doszedlem w tym zadaniu do tego ze skala podobienstwa pol

	25		5		hdluzsze		5
to k2=		wiec k=		i potem zapisalem ze		=		a
	16		4		hkrotsze		4

calkowita wysokosc to h_krotsza + h_dluzsza = 18 i wtedy jest uklad rownan ale zapomnialem o tej zaleznosci h + h =18

Kipic: ale wsumie taka maturka jak ta tez moglaby byc

Mila: Podajcie może inny adres tej matury rozszerzonej, nie mogę ściągnąć.

use: no tak ale obliczyles skale podobienstwa wiec na jakiej podstawie vto trojkaty podobne ?

Kipic: ale ktorej tej co ma 104 mb

use: mila wez ogarnij ten trapez ...

Kipic: najprosztsze rozumowanie bo to sa trojkaty ktore powstaly po przecieciu sie dwoch przekatnych a na dodattek to jest trapez wiec tym bardziej one sa podobne jak i te po bokach

use: dobra ale wolalbym jakis konkretny dowod

Kipic: wiec musza byc podobne bo przeciez jak wiemy podstawy w trapezie sa rownolegle

Kipic: no to konkretnie po przecieciu sie dwoch przekatnych sa to katy przylegle a podstawy w trapezie sa rownolegle wiec to juz wystaczy zeby powiedziec ze sa podobne

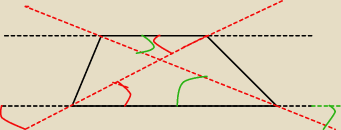
use: juz wiem :

Mila: Około 21 będę wolna, to przygotujcie pytania.

Kipic: ja mam prosbe o takie zadanie : Dla jakich wartosci parametru m pierwiastki x₁ i x₂ rownania 2x²−8mx + 4= 0 spelniaja warunek 2x₁−x₂=2 wiec wiem oczywiscie ze Δ>0 ale co z tym : 2x₁−x₂=2

Kipic: niemam pojeci jak to sprowadzic do wzorow vieta ale jedyne co mi do glowy przychodzi to to zeby policzyc m₀ z delty a potem podstawic czy tak mozna

Dominik: 2x² − 8mx + 4 = 0 Δ = 64m² − 32 = 32(2m − 1) √Δ = 4√2(2m − 1) x₁ = 2 + √2(2m − 1) x₂ = 2 − √2(2m − 1) innej opcji nie widze.

Kipic: no wlasnie tez tak myslalem zeby poprostu podstawic ale watpie czy tak mozna robic

Dominik: mozna jak najbardziej.

Dominik: nie ma zadnego nakazu uzywania wzorow viete'a; zazwyczaj ich uzywamy tylko by ulatwic rachunki.

use: mozna wzory wieta wynikaja z wzorow na pierwiastki

Kipic: hmmm jakos strasznie dziwolongi z tego wychodza

Kipic: ale skoro twierdzicie ze mozna to dobra dzieks

Dominik: wyprowadzenie wzorow viete'a ax² + bx + c = a(x − x₁)(x − x₂) = = a(x² − x₂x −x₁x + x₁x₂) = = a(x² − (x₁ + x₂)x + x₁x₂) = = ax² + −a(x₁ + x₂)x + ax₁x₂ porownuje wspolczynniki przy odpowiednich potegach x wielomianu

	−b
b = −a(x1 + x2) ⇒ x1 + x2 =
	a

	c
c = ax1x2 ⇒ x1x2 =
	a

Kipic: o kurcze grube to wyprowadzenie

Dominik: niedawno wyprowadzilem tutaj wzor na delte i pierwiastki rownania kwadratowego; nie chce mi sie szukac, mam na wlasnej stronie napisane w latex−u. http://mdzn.pl/wyroznik.html

Kipic: ooo niezle

use: po co tak wystarczy :

	b		b		b2		b2
f(x)=ax2+bx+c=a(x2+		x)+c=a(x2+		x+		)−		+c=
	a		a		4a2		4a

	b		b2−4ac
=a(x2−		)2−
	2a		4a

Kipic: jak z tego najprosciej miejsce zerowe wyznaczyc f/9x)=log₅(3x−5)+3 bo mi dziwologni wychodza

Dominik: use, masz blad. w mianowniku powinno byc 4a². poza tym nie dokonczyles. no i przyjrzyj sie − to jest dokladnie to samo (dwukrotne doprowadzenie do wzorow skroconego mnozenia).

use: log5(3x−5)=−3

	1
czyli (3x−5)=
	125

use: przyjrzyj sie dobrze bnie ma żadnego a² w mianowniku

Kipic:

	5001
no wlasnie w odpowiedzich wychodzi		tylko jak
	3000

Dominik:

	b2 − 4ac
a, no nie ma a2 bo z		nie wyciagnales a. nastepnie musisz to zrobic i
	4a

zastosowac wzorek a² − b² = (a − b)(a + b). przyjrzyj sie temu co ja napisalem − to jest DOKLADNIE to samo.

use:

	b		b2−4ac		b		Δ
a(x+		)2−		=a[(x+		)2−		]
	2a		4a		2a		4a2

use: nic ide oglądać lige mistrzow

Mila: Dla jakich wartosci parametru m pierwiastki x1 i x2 rownania 2x²−8mx + 4= 0 spelniaja warunek 2x1−x2=2 Δ=64m²−4*4*2=64m²−32 64m²−32>0

	√2		√2
2m2−1>0⇔(m−		)*(m−		)>0⇔
	2		2

	√2		√2
m∊(−∞;−		)U(		;∞)
	2		2

1) x₁+x₂=4m 2) x₁*x₂=2 3) 2x₁−x₂=2 z (1) i (3) ⇒3x₁=4m+2 x₁+x₂=4m /*3 3x₁+3x₂=12m 4m+2+3x₂=12m 3x₂=12m−4m−2 3x₂=8m−2 2) x₁*x₂=2⇔3x₁*3x₂=2*9 (4m+2)*(8m−2)=18 ⇔16m²+4m−11=0 Δ=12√5

	−1−3√5		−1+3√5
m1=		lub m2=
	8		8

dokończ, masz odpowiedź?

123: Ma ktos linki do probnych matur z rozszerzenia z CKE/OKE 2013r? (z innych stron mnie nie interesują).

Mila: http://www.zadania.info/d1507 Masz tam, Poznań, Lublin, Łomżę, Kielce..

aniabb: 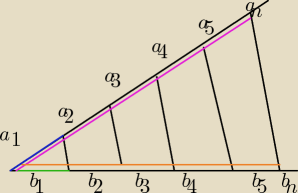Technik to zadanie z 17:31 to rozwiązuje się z Talesa praktycznie jednym rysunkiem

Technik: @aniabb jesteś genialna w życiu bym na to nie wpadł żeby zrobić to właśnie z twierdzenia Talesa

aniabb: widziałam to zadanko kiedyś tutaj bo ktoś chciał, żeby wyjaśnić dlaczego na zadania info je tak rozwiązali więc może tam znajdziesz dokładną rozpiskę jeśli chcesz, bo dla mnie wszystko jest oczywiste