Oblicz odległość punktu C od środka okręgu lolly: Dany jest okrąg o środku w punkcie O i promieniu 5 cm. Z punktu C poprowadzono dwie styczne do tego okręgu. Cięciwa AB wyznaczona przez punkty styczności ma długość 8 cm.

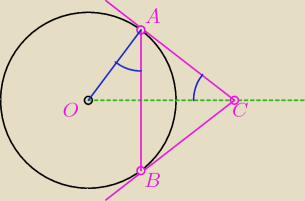
Skipper: ...popatrz ... i licz ...

lolly: dzieki

Janek191: r = 5 cm AB = 8 cm x − odległość cięciwy AB od środka okręgu O d − odległość punktu C od środka okręgu O Mamy x² + 4² = 5² x² = 25 − 16 = 9 x = √9 = 3 x = 3 cm −−−−−−−−−−− Z podobieństwa trójkątów mamy

3		4
	=
4		d − 3

3*( d − 3) = 4*4 = 16

	16
d − 3 =
	3

	16		16		9		25		1
d =		+ 3 =		+		=		= 8
	3		3		3		3		3

	1
Odp. d = 8		cm
	3

==================

leon: Czy można to zadanie zrobić na układ równań stosując dwukrotnie twierdzenie Pitagorasa?