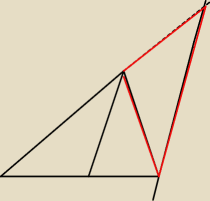
Trójkąt równoramienny na przedłużeniu prostej równoległej do dwusiecznej kąta. Grzegorz: Mam problem z rozwiązaniem jednego zadania z geometrii. Mianowicie: W trójkącie ABC poprowadź z wierzchołka B prostą równoległą do dwusiecznej kąta A przecinającą przedłużenie boku AC w punkcie D. Uzasadnij, że trójkąt DBA jest równoramienny. Z góry dzięki za pomoc.

aniabb:

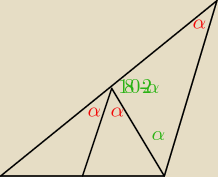
aniabb: proste równoległe więc na górze też kąt α przedłużenie prostej więc kat 180°−2α suma kątów e trójkącie 180° zatem na dole α jak dwa kąty równe to równoramienny

Grzegorz: Ok. Dzięki. Jakby ktoś miał chwilę to jeszcze jedno potrzebuję. Zbadaj zależności między miarą kąta środkowego opartego na łuku AB okręgu i kąta utworzonego przez styczne do tego okręgu.