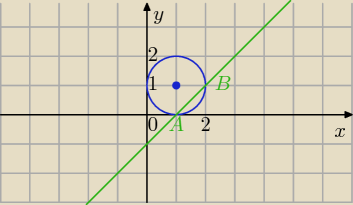
Oblicz długość cięciwy... Aneta: Oblicz długość cięciwy okręgu x²+y²−2x−2y+1=0 zawartej w prostej x−y−1=0 Proszę o pomoc

Ajtek: Zapisz równanie prostej w postaci kierunkowej, jastępnie podstaw do równania okręgu w miejsce y równanie tej prostej. Znajdziesz 2 punkty przez które przechodzi ta cieciwa. Następnie policzysz jej długość.

Aneta: nie wiem, czy wyszło mi to dobrze, jednakże dziękuję za pomoc

Ajtek: Oby dobrze .

Aneta: oby

Ajtek: A jakie masz równanie kierunkowej prostej?

Mila: x²+y²−2x−2y+1=0⇔(x−1)²−1+(y−1)²−1+1=0 (x−1)²+(y−1)²=1 postać kanoniczna S=(1,1) r=1 x−y−1=0⇔y=x−1 (0,−1), (1,0) Jaki masz wynik? |AB|=√2

Ajtek: Ech Mila, nie dasz mi podręczyć dziewczyny .

Mila: OJj! To idę spać.Dobranoc

Ajtek: Do zobaczenia [N{Mila]] . Spokojnych

Aneta: widzę, że troszkę mnie ominęło zadania mnie pochłonęły trochę inaczej mi wyszło, równanie kierunkowej prostej dobrze miałam, dziękuję Mila Tb Ajtku również mimo, że chciałeś mnie pomęczyć Również życzę miłej nocki.

Ajtek: To pomęczę jeszcze chwilę: Gdy mamy do czynienia z połączeniem wyrazowym mimo że lub mimo iż, przecinek stawiamy przed całym tym połączeniem (o ile nie znajduje się na początku zdania), nigdy zaś przed słowem że ani iż

Godzio: A ja mam zawsze dylemat na wykładach: "taka że" , na każdym wykładzie mam to wyrażenie i 3/4 wykładowców pisze: taka, że a prawie nikt , taka że A poprawna jest 2 forma nie ?

Ajtek: Godzio, nie męcz mnie Idę spać. Spokojnej nocy Wszystkim .

Aneta: dobrze...będę na przyszłość pamiętać...thx Dobranoc

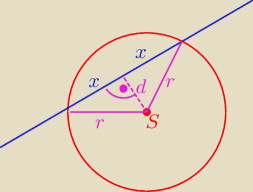
Gustlik: Oblicz długość cięciwy okręgu x²+y²−2x−2y+1=0 zawartej w prostej x−y−1=0 Proszę o pomoc Można bez układu równań: Obliczam współrzędne środka i promień okręgu ze wzorów: x²+y²+Ax+By+C=0

	A		−2
a=−		=−		=1
	2		2

	B		−2
b=−		=−		=1
	2		2

r=√a²+b²−C=√1²+1²−1=√1=1 Odległość środka okręgu od prostej:

	|Ax0+By0+C|
d=
	√A2+B2

	|1−1−1|		|−1|		√2
d=		=		=
	√12+(−1)2		√2		2

Z tw. Pitagorasa − obliczam x: r²=x²+d²

	√2
12=x2+(		)2
	2

	1
1=x2+
	2

	1
x2=		/√
	2

	√2
x=
	2

Odp. dł. cięciwy=2x=√2