trójkąt równoboczny kate : Podstawa trójkąta równoramiennego ma długość 12 cm a wysokość opuszczona na tę podstawę ma długość 8 cm .Odległość od środka tej wysokości do ramienia trójkąta jest równa ?

ICSP: 2,4

kate : a czy możesz mniej więcej napisać jak to obliczyłeś ?

Mila: |CB|²=6²+8² |CB|=10 ΔCEP∼ΔBCD⇔

PE		DB
	=		⇔
CP		CB

x		6
	=
4		10

x=2,4

kate : dziękuje bardzo za pomoc

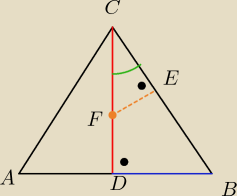ICSP: |AB| = 12 ⇒ |BD| = 6 |CD| = 8 ⇒ |CF| = 4 |BC| = 10 ( z twierdzenia Pitagorasa dla Δ CDB) teraz ∡BDC = ∡ CEF oraz ∡BCD = ∡ ECF z tego oraz z informacji że suma miar kątów w trójkącie jest równa 180 wynika że ∡ DBC = ∡ CFE zatem ΔBDC ma takie same kąty co Δ ECF. Jak mają te same kąty to są na mocy cechy kkk podobne. Stosunek odpowiednich odcinków jest zatem równy :

|EF|		|CF|
	=
|BD|		|BC|

dokończ

zajączek: Z podobieństwa trójkątów DBC i SEC

	6		10
		=		⇒ x= ...
	x		4

zajączek: Ale :sypnęło"

Mila: