wykres funkji matura 2010 Alois~:

	1
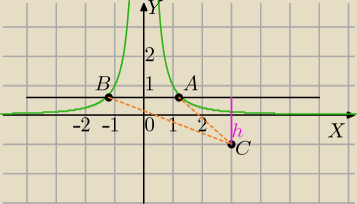
Wykres przedstawia f(x)=
	x2

Przeprowadzono prostą równoległą do osi Ox , która przecięła wykres tej funkcji w punktach A i B . Niech C = (3,− 1). Wykaż, że pole trójkąta ABC jest większe lub równe 2.

	1
i teraz moje pytanie oznaczyłam że A B maja wspołrzedne odpowiednio (−x,		) i
	x2

	1
(x,		)
	x2

skorzystałam z wzoru na pole i coś nie moge się doliczć.

	1		1		1		1
P =		|(x+x)2 (−1−		)− (		−		)2(3+x)2|
	2		x2		x2		x2

	1
|x+2+		|≥1
	x2

czy to jest dobrze ?

Alois~: zjadło mi coś

	1
|x2 + 2 +		| ≥1
	x2

Alois~: ponawaiam

Mila:

	1
A=(x,		) i x≠0
	x2

	1
B=(−x,		)
	x2

	1
PΔ=		*|AB|*h
	2

	1		1		1
PΔ=		*|2x|*(1+		)=|x|*(1+		)
	2		x2		x2

	1
PΔ=|x|+		≥2 ponieważ
	|x|

Uzasadnienie:

	1
|x|+		≥2 /*x⇔
	|x|

|x|²+1≥2|x|⇔ |x|²−2|x|+1≥0⇔ (|x|−1)²≥0 nierówność prawdziwa

Alois~: dzięki Mila a tym moim sposobem też chyba powinno wyjsc podobnie czy cos poplatalam ..

Mila: tak, pokręciłaś. popraw zapisy.