:) arwena: hej mam problem z takimi zadaniami 1. Jak narysować zbiór punktów: (x − |x|)² + (y − |y|)² ≤ 4? Czy to koło należy narysować o środku w punkcie (0, 0) i tylko w 1. ćwiartce? 2. Dany jest trapez ABCD o podstawach AB i CD. Przekątne trapezu przecinają się w punkcie S. Pole trójkąta ABS jest równe P₁, a pole trójkąta CDS wynosi P₂. Oblicz pole trapezu. Wyszło mi, że P = ¹₂*|AD|*|BD|*sinα (α to kąt |ASB|), ale to chyba zła odpowiedź, bo wydaje mi się, że pole trapezu powinno zawierać P₁ i P₂

sushi_ gg6397228: 1. jeżeli x, y są dodatnie to masz... jeżelo x,y są ujemne to masz...

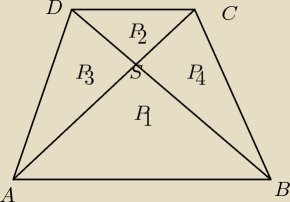
irena_1: Trójkąty ABS i CDS są podobne s− skala podobieństwa

	|SC|
s=
	|SA|

	P2
s2=
	P1

Trójkąty ADS i CDS mają wspólną wysokość poprowadzoną na prostą AC

P3		|AS|		1		P1
	=		=√		=√
P2		|CS|		s		P2

P₃=√P₁P₂ P₄=P₃ P_ABCD=P₁+P₂+2√P₁P₂

arwena: dzięki

irena_1: I ćwiartka x>0 i y>0 (x−x)²+(y−y)² ≤ 4 0 ≤ 4 Całe wnętrze tej ćwiartki II ćwiartka x<0 i y>0 (x+x)²+(y−y)² ≤ 4 4x² ≤ 4 x² ≤ 1 −1≤x≤0 Na prawo od prostej x=−1 do dodatniej półosi OY, razem z tą półosią III ćwiartka x<0 i y<0 (x+x)²+(y+y)² ≤ 4 4x²+4y² ≤ 4 x²+y² ≤ 1 Ćwiartka koła o środku (0, 0) i promieniu 1 IV ćwiartka x>0 i y<0 (x−x)²+(y+y)² ≤ 4 4y² ≤ 4 y² ≤ 1 −1 ≤ y≤ 0 W górę od prostej y=−1 do dodatniej półosi OX razem z tą półosią

zajączek: Bardziej "elegancki" wzór P(tr)= (√P₁+√P₂)²

arwena: dzięki