geometria analityczna - zadanie maturalne
Zosia:
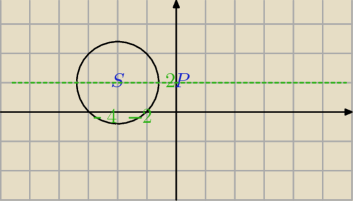
dany jest okrąg o równaniu (x+4)
2 + (y−2)
2= 7. Wyznacz równanie prostej stycznej do tego
okręgu, przechodzącej przez punkt P=(0,2).
środek koła posiada współrzędne S(−4, 2) oraz promień r=
√7
punkt P oraz S posiadają wspólną współrzędną y=2 więc leżą na tej samej prostej
więc prosta styczna do okręgu posiada współrzędne x= 4 −
√7
1 kwi 13:27
ICSP: ...
i ze niby x = 4 −
√7 przechodzi przez punkt P

1 kwi 13:28
Zosia: tutaj jest nie spójność. Z definicji prosta styczna ustawiona jest pod katem prostym do
promienia okręgu oraz posiada z nim 1 punkt wspólny w tym wypadku jest to nie możliwe. Czy
popełniałam błąd?
1 kwi 13:43
ICSP: a to prosta nie może być już ukośna

1 kwi 13:50
ICSP:
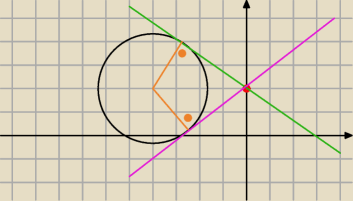
1 kwi 13:52
pigor: ... , np. tak :niech y−2=m(x−0) ⇔
y=mx+2 − szukane równanie stycznej, to
z równania okręgu (x+4)
2+(mx+2−2)
2=7 ⇔ x
2+8x+16+m
2x
2−7=0 ⇔
⇔ (m
2+1)x
2+8x+9=0 − równanie kwadratowe zmiennej x będzie miało 1 rozwiązanie ⇔
⇔ Δ=64−36(m
2+1)=0 ⇔ m
2+1=
6436 ⇔ m
2=
2836 ⇔ |m|=
79 ⇔
⇔ m=−
13p{7 lub m=
13√7 , więc masz
y= ±13√7x+2 −szukane równania
stycznych do okręgu ⇔
√7x−3y+6=0 lub
√7x+3y−6=0 w postaci ogólnej. ...

1 kwi 14:26
 dany jest okrąg o równaniu (x+4)2 + (y−2)2= 7. Wyznacz równanie prostej stycznej do tego
okręgu, przechodzącej przez punkt P=(0,2).
środek koła posiada współrzędne S(−4, 2) oraz promień r= √7
punkt P oraz S posiadają wspólną współrzędną y=2 więc leżą na tej samej prostej
więc prosta styczna do okręgu posiada współrzędne x= 4 − √7
dany jest okrąg o równaniu (x+4)2 + (y−2)2= 7. Wyznacz równanie prostej stycznej do tego
okręgu, przechodzącej przez punkt P=(0,2).
środek koła posiada współrzędne S(−4, 2) oraz promień r= √7
punkt P oraz S posiadają wspólną współrzędną y=2 więc leżą na tej samej prostej
więc prosta styczna do okręgu posiada współrzędne x= 4 − √7



