
 jak pewnie zauważyłaś − lubie te zadania − można rysować i jeszcze liczyć całki − czego chcieć
więcej
jak pewnie zauważyłaś − lubie te zadania − można rysować i jeszcze liczyć całki − czego chcieć
więcej  wybór punktu możemy sprowadzić do wyboru kąta:
losujemy kąt α − kąt jaki tworzy prosta OX z prostą OA i β kąt OX i OB
(tzn losujemy punkt, ale bierzemy jego kąt)
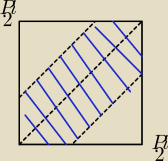
Ω = [0,π2]2
(α,β) ∊ [0,π2]2
| α − β | < π4
β − π4 < α < β + π4
Z − kąt jest mniejszy od π/4
wybór punktu możemy sprowadzić do wyboru kąta:
losujemy kąt α − kąt jaki tworzy prosta OX z prostą OA i β kąt OX i OB
(tzn losujemy punkt, ale bierzemy jego kąt)
Ω = [0,π2]2
(α,β) ∊ [0,π2]2
| α − β | < π4
β − π4 < α < β + π4
Z − kąt jest mniejszy od π/4
| π | π | π | ||||
|Z| = ( | )2 − ( | − | )2 | |||
| 2 | 2 | 2√2 |

| π | π | π | ||||
|Z| = ( | )2 − ( | − | )2 | |||
| 2 | 2 | 4 |

 tylko raczej ciężko by mi było wpaść na to, że Ω=[0,π2]2 tzn wiem, że to pierwsza
ćwiartka, więc muszą należeć od 0 do π2, ale chodzi mi bardziej o to, że nie bardzo
ogarniam skąd mam wiedzieć, że to akurat kwadrat musi wyjść
tylko raczej ciężko by mi było wpaść na to, że Ω=[0,π2]2 tzn wiem, że to pierwsza
ćwiartka, więc muszą należeć od 0 do π2, ale chodzi mi bardziej o to, że nie bardzo
ogarniam skąd mam wiedzieć, że to akurat kwadrat musi wyjść druga sprawa, przy wyliczaniu Z trochę się pogubiłam.. a konkretniej,. ok, pole kwadratu to
π24 .. ale nie za bardzo ogarniam, skąd pole tych trójkątów to (π2 − π4)2.
wiem, że pewnie zagmatwałam i może do końca nie wiem o co mi chodzi.. ale chyba o to, że skąd
ten kwadradrat wziął
wiem, że motam.. siebie i innych, głośno myślę
druga sprawa, przy wyliczaniu Z trochę się pogubiłam.. a konkretniej,. ok, pole kwadratu to
π24 .. ale nie za bardzo ogarniam, skąd pole tych trójkątów to (π2 − π4)2.
wiem, że pewnie zagmatwałam i może do końca nie wiem o co mi chodzi.. ale chyba o to, że skąd
ten kwadradrat wziął
wiem, że motam.. siebie i innych, głośno myślę 
 Nie ma sprawy
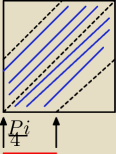
Nie ma sprawy  Ma wyjść kwadrat bo obydwa punkty są losowane z tego samego zbioru
czyli kąt dla α (pierwszego punktu) jest losowany z tej samej dziedziny co kąt β (dla drugiego
punktu) czyli [0,π/2]. zatem para (α,β) jest z [0,π/2]2
Potraktowałem pole 2 niezakolorowanych trójkątów jako jeden kwadrat (są przystające,
równoramienne). Taki skrót w obliczeniach
Ma wyjść kwadrat bo obydwa punkty są losowane z tego samego zbioru
czyli kąt dla α (pierwszego punktu) jest losowany z tej samej dziedziny co kąt β (dla drugiego
punktu) czyli [0,π/2]. zatem para (α,β) jest z [0,π/2]2
Potraktowałem pole 2 niezakolorowanych trójkątów jako jeden kwadrat (są przystające,
równoramienne). Taki skrót w obliczeniach 
| π | π | |||
Przyprostokątna niezakolorowanego trójkąta ma długość: | − | |||
| 2 | 4 |
| π | π | |||
zatem pole niezakolorowanego trojkąta: 12( | − | )2 | ||
| 2 | 4 |
