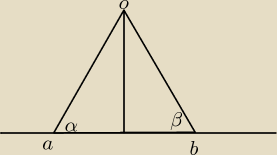
 Balon znajdował się na równinie pomiędzy dwoma obserwatorami A i B, stojącymi w odległości 110
m od siebie. W pewnej chwili balon zaczął się unosić pionowo do góry (rysunek powyżej). Po
pewnym czasie obaj obserwatorzy jednocześnie zmierzyli kąty wzniesienia balona α = 45 stopni i
β= 60 stopni. Oblicz, na jaką wysokość uniósł się wtedy balon (oznaczony o). Przyjmij, że √3
≈ 1,75.
Balon znajdował się na równinie pomiędzy dwoma obserwatorami A i B, stojącymi w odległości 110
m od siebie. W pewnej chwili balon zaczął się unosić pionowo do góry (rysunek powyżej). Po
pewnym czasie obaj obserwatorzy jednocześnie zmierzyli kąty wzniesienia balona α = 45 stopni i
β= 60 stopni. Oblicz, na jaką wysokość uniósł się wtedy balon (oznaczony o). Przyjmij, że √3
≈ 1,75.
| h | |
= tg60o ⇒ h= (110−h)√3 ⇔ h(√3+1)= 110√3 /*(√3−1) ⇔ | |
| 110−h |

 !
!
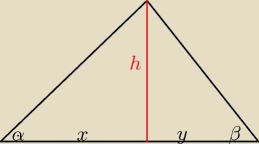 α=450, β=600
y=110−x
α=450, β=600
y=110−x
| h | |
=tg450=1 | |
| x |
| h | |
=tg600=√3 | |
| 110−x |
 !
!