prawdopodobienstwo geometryczne mamba: pare liczb (a,b) wybrano losowo z prostokata [−1,1]². oblicz prawdopodobienstwo, ze rownanie ax² + bx + 1=0 ma: a) pierwiastki rzeczywiste b) pierwiastki rowne c) pierwiastki rzeczywiste dodatnie mam problem z tym zadaniem.. pierwsza sprawa, to nie jestem pewna, czy dobrze narysowalam w ukladzie wspolrzednych, dlatego dolaczam rysunek. w przypadku a) licze w ten sposob, ze przyjmuje ax² + bx + 1≥0, stad ¹₄b²≥a. z tego rysunku wychodzi mi, ze cala przesten omega=1, licze calke od −1 do 1 ii pojawia mi sie problem, bo wychodzi pole= −¹₃ b) nie wiem jak to rozwiazac, doszlam jedynie do tego, ze x₁=x₂, czyli −√Δ=√Δ c) myslalam, zeby po prostu ax² + bx + 1 >0 serio mecze te zadania,ale nie wiem jak ugryzc.. z gory dzieki!

mamba: podbijam

on: pare liczb (a,b) wybrano losowo z prostokata [−1,1]2. nie rozumiem to jest przedzial liczbowy do kwadratu ?

ff: ax²+bx+1 = 0 a ≠ 0 a) A − równanie ma dwa pierwiastki: b²−4a ≥ 0 b² ≥ 4a

	1
a ≤		b2
	4

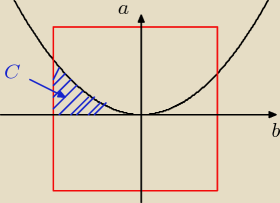
|A| = ∫₋₁^{1 1}₄b² db + 2 (część wspólna obszaru pod wykresem a = ¹₄b² i prostokąta [−1,1]² ) |A| = 2∫₀^{1 1}₄b² db + 2 = ¹₆ + 2

	13
P(A) =
	24

b) b² = 4a tutaj nie jestem pewien − ale raczej 0 (miara jordana krzywej to 0) B − dwa równe pierwiastki |B| = 0 c) dwa pierwiastki:

	1
a <		b2
	4

C − dwa różne pierwiastki rzeczywiste wzory Viete'a: (pierwiastki mają ten sam znak i ich suma jest dodatnia)

1
	> 0
a

−b
	> 0
a

czyli C jest wyznaczone przez: a > 0 b < 0

	1
a <		b2
	4

|C| = ∫₋₁^{0 1}₄ b² db = ∫₀^{1 1}₄ b² db = ¹₁₂

mamba: tak myslalam, ze padlam juz na wstepie z rysowaniem.. moglabym prosic o rade tak sie zabierac do rysowania w tego typu zadaniach? jak mialam do czynienia np ze wspolrzednymi [0,2]x[0,4] itd to "samo szlo" jak bylo to 0.. ale w innych przypadkach sie motam ii chcialabym ogarnac druga sprawa, to nie rozumiem dlaczego dodajemy 2 przy calkowaniu w podpunkcie a) ii czy moge oprocz tej przestrzeni C po lewej stronie, zaznaczyc ja tez po prawej? b) czyli w tylko tyle wystarczy? ii w C niestety,ale w odpowiedziach mam {1}{48} wielkie dzieki za odzew!

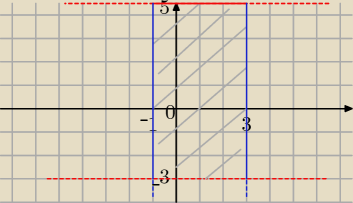
ff: Jak masz do narysowania np. [−1,3]x(−3, 5] to jest to zbiór punktów które pierwszą współrzędną mają w przedziale [−1,3] a drugą w (−3,5] − czyli rysujesz sobie na osi x przedział: [−1,3], a na osi y: (−3,5] ogólniej: AxB = { (a,b) | a ∊ A ∧ b ∊ B } w a) dodajemy jeszcze 2 bo to jest połowa pola prostokąta (całka da nam jedynie pole pomiędzy wykresem a osią y=0), a obszar zdarzenia to wszystkie punkty pod wykresem w prostokącie b) powinno − prosta/krzywa ma grubość 0 w c) nie − tylko jedna strona: z warunków a>0,b<0 (dają nam pierwiastki dodatnie)

	|C|		1
i jest prawidłowo: P(C) =		=
	|Ω|		48

mamba: wielkie dzieki! w tym c) to moje niedoczytanie, bo zapomnialam podzielic przez pole tego kwadratu w sumie to nie jest takie trudne,ale sama bym nie wpadla na to.. szczegolnie, zeby jeszcze 2 dodac.. w kazdym razie czcze Cie w +∞