trygonometria Iwona:

	1
Wyznacz wartości parametru m dla których (		cosx−m)(2sinx−3m+2)=0 ma rozwiązanie x∊(π,2π)
	2

Iwona: cosx=2m v

	3m−2
sinx=
	2

i dalej nie wiem... : (

Dominik: no i wiemy ze w III i IV cwiartce sinus przyjmuje wartosci ujemne, a kosinus i ujemne, i dodatnie.

Iwona: czyli ukladam nierówność dla sinusa 3m−2<0 ? i dla kosinusa 2m>0 lub 2m<0 dobrze rozumiem?

Dominik: spojrz na wykres funkcji sinus i kosinus. sinus chyba nie moze przyjac wartosci −5, prawda? a ty miedzy innymi taka dopuscilas.

Iwona: patrzę na wykres funkcji sinus i kosinus i w tym przedziale tylko kosinus moze być równy zero

	3
dla		π o tym mówisz?
	2

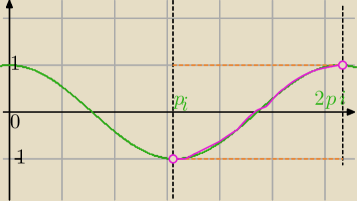
Mila: 1) funkcja y=cosx dla x ∊(π,2π) przyjmuje wartości y∊(−1,1) cosx=2m⇔ −1<2m<1⇔

−1		1
	<m<
2		2

bezendu: Mil miałaś mi dać pod koniec tygodnia przykład na tą wartość bezwzględną

Iwona: czyli to jest właściwie "nierównośc" trygonometryczna.

	−4		−2
dla sinusa		<m<
	3		3

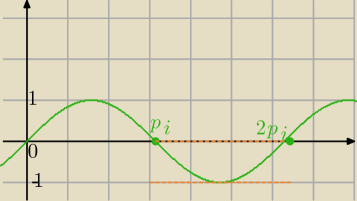
Mila: 2) (2sinx−3m+2)=0⇔ 2sinx=3m−2

	3m−2
sinx=
	2

Funkcja y=sinx dla x∊(π,2π) przyjmuje wartości y∊<−1,0)

	3m−2
−1≤		<0 /*2
	2

−2≤3m−2<0 /+2 0≤3m<2 /:3

	2
0≤m<
	3

Mila: Do Bezendu Załóż nowy post, to wpiszę, gdzieś Ci już wpisałam, ale ktoś rozwiązał.