Prosba Marta: Hej.mam 5 zadan m.in. Z twierdzen sinusow. Pomóżcie ? Ńie mam o nich pojęcia ...

zajączek: https://matematykaszkolna.pl/strona/549.html

marta: jak kopiować wzory z worda?

Dominik: niestety trzeba przepisac

marta: sprawdz czy podana równosć jest tożsamością trygonometryczną:

	1		1
(1+ cosα) (		−		) = sinα
	sinα		tgα

Dominik: no i co z tym fantem zrobisz? nie musze chyba mowic ze musisz poprzeksztalcac lewa strone. zacznij od dodania ulamkow w obu nawiasach.

marta: Balon znajdował się na równinie pomiędzy dwoma obserwatorami A i B, stojącymi w odległości 110 m od siebie. W pewnej chwili balon zaczął się unosić pionowo do góry (rysunek poniżej). po pewnym czasie obaj obserwatorzy jednocześnie zmierzyli kąty wzniesienia balona α = 45 stopni i β= 60 stopni. Oblicz, na jaką wysokość uniósł się wtedy balon (oznaczony o. Przyjmij, że √3 ≈ 1,75.

marta: Dominik, pls, jeżeli wiesz jak to zrobić to mi napisz rozwiązanie. zupełnie nie wiem jak to przekształcać.

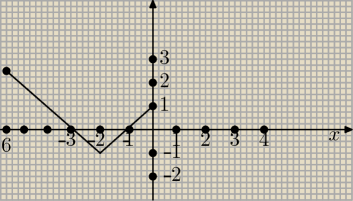
marta: Poniżej przedstawiony jest wykres funkcji f. Na podstawie wykresu funkcji podaj dziedzinę, zbiór wartości funkcji, miejsca zerowe funkcji oraz zbiór tych argumentów, dla których funkcja osiąga wartości dodatnie.

Dominik: a umiesz dodawac ulamki?

marta: Umiem, ale nie gdy w liczniku i mianowniku mam sinusy i tangesy. Generalnie to zadania ze szkoły mojego brata, który jest niewidomy. Ja edukację na tym poziomie mam dawno za sobą i mało pamiętam, dlatego tu się zgłosiłam.

marta: chcę mu pomóc

zajączek:

	sinα		1		cosα
tożsamość: tgα=		to		=
	cosα		tgα		sinα

oraz z jedynki trygonometrycznej sin²α+cos²α=1 to 1−cos²α= sin²α

	1		cosα		1−cosα		(1+cosα)(1−cosα)
L= (1+cosα)*(		−		)=(1+cosα)*(		)=		=
	sinα		sinα		sinα		sinα

	1−cos2α		sin2α
=		=		= sinα
	sinα		sinα

L=P

marta: dziękuję serdecznie!

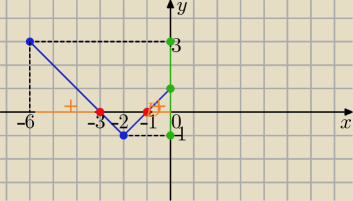
zajączek: D_f= <−6, 0> ZW=<−1,3> miejsca zerowe x= −3 v x= −1 f(x) >0 ⇔ x€ <−6,−3) U (−1,0>

marta: określ dziedzinę funkcji

	√3−2x
f(x) =
	x2−4

marta: Wykres funkcji f(x) = 2x − 3, x∊R, przekształcono przez symetrię osiową względem osi OX i otrzymano wykres funkcji y=g(x) a) Podaj wzór funkcji y = g(x). b) Oblicz miejsce zerowe funkcji y=g(x)

zajączek: 3−2x≥0 i x²−4≠0 −2x≥−3 i (x−2)(x+2)≠0 x≤ 1,5 i (x≠2 v x≠ −2) D= (−∞, −2) U (−2; 1,5>

marta: A uwzględniony jest tutaj pierwiastek, który występuje w liczniku 3 − 2x ? przepraszam, ale wolę zapytać

zajączek: tak .... 3−2x≥0

marta: dzięki

zajączek: g(x)= −f(x)= −(2x−3)= −2x+3 g(x)=0 ⇔ −2x+3=0 ⇔ x=1,5

marta: jeszcze zostało z tym balonem, jeżeli byłoby możliwe to bardzo proszę o pomoc ...

zajączek: Z jakim "balonem" ? na Sylwestra?

marta: Balon znajdował się na równinie pomiędzy dwoma obserwatorami A i B, stojącymi w odległości 110 m od siebie. W pewnej chwili balon zaczął się unosić pionowo do góry (rysunek poniżej). po pewnym czasie obaj obserwatorzy jednocześnie zmierzyli kąty wzniesienia balona α = 45 stopni i β= 60 stopni. Oblicz, na jaką wysokość uniósł się wtedy balon (oznaczony o. Przyjmij, że √3 ≈ 1,75. rysunek powyżej