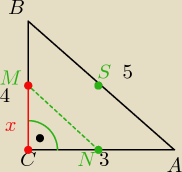
Dominik: Boki trójkąta prostokątnego ABC mają długości: |AC| = 3, |BC| = 4, |AB| = 5. Prosta l, równoległa do prostej AB, przecina boki AC i BC odpowiednio w punktach M i N. Niech S oznacza środek odcinka AB oraz |MC| = x. a) Pole P(x) trójkąta MNS jest funkcją zmiennej x. Znajdź wzór tej funkcji. b) Zbadaj, jaką największą wartość może przyjmować pole trójkąta MNS.

	5
jedyne co zrobilem to wyznaczylem |MN| =		x. jakies pomysly?
	3

mmm:

Dominik: punkty M i N nalezy oznaczyc w inny sposob (odwrotnie)

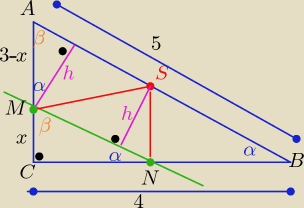
zajączek: Założenie x€(0,3) Teraz "poćwicz " z podobieństwami odpowiednich trójkątów

	2
otrzymasz; P(x)=−		x2+2x
	3

Dominik: okej, mam.

	x
ΔNCM ~ ΔABC, k =
	3

P_ΔABC = 6

	x
PΔNCM = (		)2 * 6
	3

P_ΔNBS = P_ΔAMS = 3 − x

	x		2
PΔMNS = 6 − (		)2 * 6 − 2(3 − x) = −		x2 + 2x
	3		3

Dominik: @zajaczek, dzieki. stad moznaby policzyc to szybciej znajac wysokosc trojkata MNS. dzieki.

zajączek: