trapez
Kasia: Przekątna trapezu równoramiennego ma długość 15 cm a odcinek łączący środki ramion tego trapezu
ma 12 cm
a) wyznacz wysokość trapezu
b) Oblicz pole trapezu
c) Czy miara kata ostrego trapezu może być równa 30 stopni? Odp uzasadnij.
Mam problem tylko z punktem c) Proszę o pomoc

31 mar 15:12
zajączek:
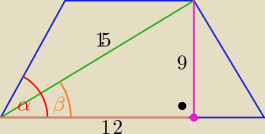
wniosek ...... podaj sama
31 mar 15:19
Kasia: Czyli sinα=2*36=72 stopnie bo przekątna w trapezie równoramiennym jest dwusieczną kąta więc
dzieli go na dwie równe połowy, stąd kąt ten ma miarę 72 stopnie?
31 mar 15:27
zajączek:
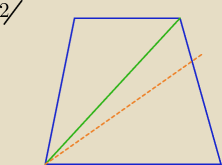
To co napisałaś nie jest prawdą ( zobacz 2 rys
Uzasadnienie do tego zadania: α=β+ "coś"= 36
o+"coś" ≠ 30
o
31 mar 15:41
asdf:
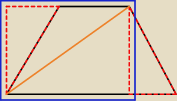
ma, zobacz. Z tego trapezu zbudujesz prostokąt, a wtedy już nie ma wątpliwości

Prostokąt lekko powiększyłem − zeby nie zamazać rysunku
31 mar 15:42
asdf: a nie, tak nie jest − wprowadziłem Cie w błąd

31 mar 15:46
Kasia: a jak powinno być?

31 mar 15:50
zajączek:
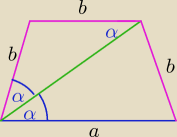
31 mar 15:56
Kasia: A skąd wiemy że górna podstawa ma taką samą długość jak ramię?
31 mar 15:58
zajączek:
Trójkąt ACD jest równoramienny ( oznacz trapez literkami ABCD
31 mar 15:59
Kasia: Rozumiem, a jak uzasadnić tą miarę kąta?
31 mar 16:01
zajączek:
zobacz drugi wpis 15:41
31 mar 16:41
Kasia: Dziękuję

31 mar 16:44
Kasia: Ale mam jeszcze pytanie w odpowiedzi jest napisane, że nie bo tgα>3/4>√33
Nie rozumiem czemu tak, jak tego tgα znaleźć?
31 mar 16:45
zajączek:

31 mar 16:45
zajączek:
Na to samo wychodzi

| | 9 | | 3 | | √3 | |
tgβ= |
| = |
| oraz tgα= tg30o = |
| |
| | 12 | | 4 | | 3 | |
31 mar 16:59
Kasia: A mogę zaznaczyć oba to kąty i napisać, że skoro tgβ=
34 a tgα jest od niego większy (co
widać na rysunku), to tgα>
34>
√33?

31 mar 17:06


 To co napisałaś nie jest prawdą ( zobacz 2 rys
Uzasadnienie do tego zadania: α=β+ "coś"= 36o+"coś" ≠ 30o
To co napisałaś nie jest prawdą ( zobacz 2 rys
Uzasadnienie do tego zadania: α=β+ "coś"= 36o+"coś" ≠ 30o
 ma, zobacz. Z tego trapezu zbudujesz prostokąt, a wtedy już nie ma wątpliwości
ma, zobacz. Z tego trapezu zbudujesz prostokąt, a wtedy już nie ma wątpliwości  Prostokąt lekko powiększyłem − zeby nie zamazać rysunku
Prostokąt lekko powiększyłem − zeby nie zamazać rysunku






