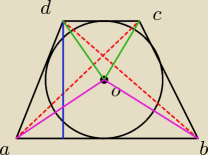
HArdcorowo Kipic: W czasie robienia zadań trafiłem na hardcorowe zadanie które mnie zagięło. Na okręgu o środku O opisano trapez równoramienny ABCD, w którym AB i CD są podstawami i lABl>lCDl . Oblicz pole i długość przekątnej tego trapezu jeśli wiadomo że lOBl=20 i lOCl−15. wiec robie rysuneczek zielone mają po 15 fioletowe mają po 20 i powiem szczerze ze nic nie widze prosze o wskazówke

Patryk: w tym przypadku wyskosci Δocd oraz abo są równe i wynosza r

Patryk: Δ

Kipic: no wiadomo ze sa rowne wkoncu okrag jest wpisany ale jak liczyc ?

Patryk: mysle

Patryk:

r		y
	=
x		r

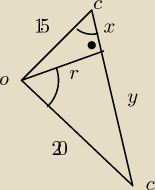
x²+r²=225 y²+r²=400

Patryk: czy pole to 600 ?

Wika: A jak to policzyłeś?

Patryk: a to twój post ?

Wika: A nie mogę zapytać?

Wika: Chciałam po prostu dowiedzieć się jak do tego doszedłeś, ale jeśli nie chcesz to nie mów

Patryk: napisałem układ z 3 niewiadomymi i rozwiazałem

Kaja: Patryk a skąd się wzięło to pierwsze równanie?

Patryk: widzisz zaznaczone katy na rysunku ?

Wika: Z podobieństwa trójkątów Kaja

Karola: Uła, to może i ja się przyłaczę

Patryk: musze przyznać ,ze przy rozwiązywaniu tego układu wspomogłem się kalkulatorem, wolfram

Kaja: Wika a skąd wiemy, że te trójkąty są podobne?

jikA: x² + r² = 225 y² + r² = 400 xy = r² {x² + xy = 225 {y² + xy = 400 _____________+ x² + 2xy + y² = 625 (x + y)² = 625 x + y = 25 ⇒ y = 25 − x r² = x(25 − x) x² + 25x − x² = 225 25x = 225 ⇒ x = 9 y = 16. Nie wiem czy dobrze sprawdźcie.

Kaja: na podstawie jakiej cechy można wywnioskować że są podobne?

Patryk: jikA wolfram tez tak obliczył

Wika: Kaju, spójrz na rysunek, Patryk poprowadził promień r, który utworzył z ramieniem |cb| kąt 90 stopni. Zaznaczył także kąty, które mają te same miary dlatego też te trójkąty są podobne, bo spełniają regułę (kąt, bok, kąt)

Kaja: Wika, tylko na jakiej podstawie te kąty mają równe miary? Rozumiem, że tak by było gdyby trójkąt ABC był prostokątny, ale przecież on chyba nie musi być prostokątny.

jikA: Czyli ten układ aż taki trudny nie jest do obliczenia.

Kaja: dobra Wika, faktycznie te trójkąty są podobne

Wika: Obliczenia jjiki dowodzą ze kat cob jest prosty

Wika: i to się zgadza

Wika: mi pole wychodzi 325

Wika: a nie, jednak 600

sinus: mam pytanie a ile wynosi długość tej przekątnej chodzi mi o wynik a wyznaczyc spróbuje sam?

sinus: wychodzi mi ze AC = √1201 [j]

Mila: Ważne ! Otóż, w tym zadaniu wykorzystujemy, to, że ΔCOB jest prostokątny ( często dają to do udowodnienia, zatem przeprowadź dowód, w zadaniu wykorzystujesz bez dowodu). 1) Możemy obliczyć, długość ramienia. CB²=20²+15²=625 CB=25

	1
2) PΔ=		*20*15=150
	2

3) Promień prostopadły do ramienia to wysokość tego Δ opuszczona na ramię.

	1
PΔ=		*25*r
	2

1
	*25*r=150⇔r=12
2

h_trapezu=2r=24 a+b=2*25=50

	50
Ptrapezu=		*24=25*24=600
	2

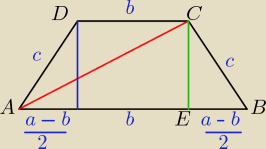
sinus: dowód zrobiłem i pole też mam wyznaczone i wszystko to co napisałaś tzn obliczenia mam tak samo tylko nie wiem co z tą przekątną bo wychodzi mi AC = √1201 i nie wiem czy to dobrze a wyznaczyłem to w nastepjący sposób; no i tak wiemzy ze AB + CD = AD +BC = 2*AD = 2*BC jak wiemy BC = 25 czyli AE = ^{a − b}₂ + b = ^{a + b}₂ AE = 25 CE = 2*r = h = 24 i teraz z twierdzenia Pitagorasa AC² = AE² + CE² AE=√625 + 576 czyli AE = √1201 dobrze?

Mila: W porządku. Sinus

sinus: okey dziękuje

XYZ: AB + CD = AD +BC = 2*AD = 2*BC jak wiemy BC = 25 czyli AE = a − b2 + b = a + b2 AE = 25 CE = 2*r = h = 24 i teraz z twierdzenia Pitagorasa AC2 = AE2 + CE2 AE=√625 + 576 czyli AE = √1201