BAAARDZO PROSZĘ O POMOC to ja ;): 1. W sześciokącie foremnym różnica długości dwóch przekątnych wychodzących z jednego wierzchołka wynosi 6 cm. Oblicz pole tego sześciokąta. 2. Na sześciokącie foremnym opisano okrąg i w ten sześciokąt wpisano okrąg. Pole powstałego pierścienia jest równe 2πdm². Oblicz pole powierzchni sześciokąta.

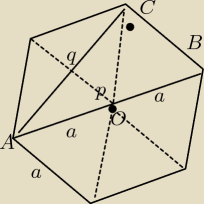
AS: Dane: p − q = r (= 6 cm) Odcinek AB = 2*a ∠ACB = 90^o bo jest wsparty na średnicy okręgu opisanego na trójkącie ABC p = 2*a , q = √AB² − BC² = √4*a² − a² = a*√3 Wstawiam do warunku w zadaniu

	r
2*a − a*√3 = r ⇒ a*(2 − √3) = r ⇒ a =
	2 − √3

Znoszę niewymierność w mianowniku a

	r		r		2 + √3
a =		=		*
	2 − √3		2 − √3		2 + √3

	r*(2 + √3)
a =		= r*(2 + √3)
	4 − 3

Pole sześciokąta składa się z 6 trójkątów równobocznych o boku a

	a2*√3		3*√3
P = 6*		=		*r2*(2 + √3)2
	4		2

	3*√3		3*√3
P =		*r2*(4 + 4*√3 + 3) =		*r2*(7 + 4*√3)
	2		2

	3
P =		*r2*(7*√3 + 12)
	2

Po podstawieniu r = 6 P = 54*(7*√3 + 12)

to ja ;): bardzo dziękuję

patrykos428: ź;e to jesty pale dostałęm

patrykos428: aδfπgΩh∞≤j≥j∊k∫k→k∑♥♥♥ ∟∀⬡