Kwadrat o boku a zgięto....
dziku: Kwadrat o boku a zgięto wzdłuż przekątnej w taki sposób, że jego dwie połowy utworzyły kąt
dwuścienny o mierze α. Odległość między wierzchołkami kwadratu nieleżącymi na krawędzi kąta
| | √2 | |
dwuściennego jest równa a √1+ |
| . Oblicz miarę kąta dwuściennego. |
| | 2 | |
30 mar 14:33
Mila:
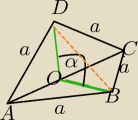
|AC|=d=a
√2
|DB|=a
√1+√2/2
skorzystaj z tw. cosinusów w ΔDOB
30 mar 16:15
krystek: Milu , witaj. Świeta już przygotowane?Spójrz na zadanie Fan
Nie widzę triku jak wyznaczyć dalej: a+b+c+d=3c+3a
30 mar 16:18
Mila:
Pozdrawiam, Krystek. Wesołych świąt!
Jeszcze tylko babki ( drożdżowe) zostały, ale chcę mieć świeżutkie jutro rano, to za godzinę
będę piekła.
Zadanie zobaczę.
30 mar 16:56
 |AC|=d=a√2
|DB|=a√1+√2/2
|AC|=d=a√2
|DB|=a√1+√2/2