pytanie
Bartek:
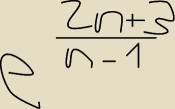
ma pytanie:
granica a
n=(1+
1n)
n=e
po przekształceniach w zadaniu wychodzi mi to co na rysunku
e
span style="font-family:times; margin-left:1px; margin-right:1px">
2n+3n−1
czy to jest = a
n gdy a>1
to wtedy granica jest nieskończoność

bo sam wykładnik dąży do 2
jak to rozwiązać?
30 mar 14:23
Bartek: chodzi o taki przykład:
lim {n+1n−1}2n+3
n→∞
30 mar 14:26
huehuehue: a moglbys napisac jaka granice liczysz ?(bez swoich przeksztalcen) jak Ci sie nie chce
| | 2n+3 | |
to zbadaj granice wykladnika czyli |
| przy n−−>∞ |
| | n−1 | |
30 mar 14:28
Bartek: przykład w poście wyzej granica wykładnika to bedzie 2 czyli wyjdzie e
2
?
30 mar 14:30
huehuehue: ok nie bylo pytania
| | n+1−2+2 | | 2 | |
limn−−−>∞ ( |
| )2n+3 = [(1+ |
| )n−1]2n+3n−1 = e4 |
| | n−1 | | n−1 | |
30 mar 14:32
Bartek: dlaczego e
4
?
wykładnik wg mnie dąży do 2 a nie do 4
30 mar 14:37
huehuehue: owszem ale wnetrze dazu do e2 ze wzoru ktory sam podales na poczatku
czyli masz (e2)limn−−>∞2n+3n−1 czyli (e2)2=e4
30 mar 14:41
Bartek: to co jest w nawiasie [ ] w Twoim poście z 14.32 daży do ewykładnik
sam wykładnik dąży do 2 czyli całość e2
30 mar 14:49
Bartek: [e]wykładnik
30 mar 14:50
huehuehue: bzdura popatrz jeszcze raz na wzor. Podam Ci jesze jeden ktory radze zapamietac
30 mar 14:53
Bartek: no tak ja ma wzór bez a w liczniku
lim (1+1n)n=e
n→∞
30 mar 14:56
Bartek: teraz to ma sens , wykładowca podałtylko to a na liście zadań potrzebny jest inny , dzięki
30 mar 14:57
Bartek: ale sam rozwiazał przykład
lim (1+53n)7n i wyszło mu e353
n→∞
30 mar 14:59
Bartek: czyli pomylił się

?
30 mar 15:00
huehuehue: nie, rozwiazanie jest poprawne
| | 5 | |
[(1+ |
| )3n]7n3n =(e5)73 |
| | 3n | |
30 mar 15:07
Bartek: już kumam dzięki
tam wykładnik po wymnozeniu powinien wyjść mi
e4n+6n−1
30 mar 15:13
Bartek: czyli e
4 dziękuje za cierpliwość

30 mar 15:13
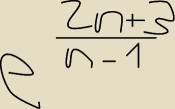 ma pytanie:
granica an=(1+1n)n=e
po przekształceniach w zadaniu wychodzi mi to co na rysunku
espan style="font-family:times; margin-left:1px; margin-right:1px">2n+3n−1
czy to jest = an gdy a>1
to wtedy granica jest nieskończoność
ma pytanie:
granica an=(1+1n)n=e
po przekształceniach w zadaniu wychodzi mi to co na rysunku
espan style="font-family:times; margin-left:1px; margin-right:1px">2n+3n−1
czy to jest = an gdy a>1
to wtedy granica jest nieskończoność bo sam wykładnik dąży do 2
jak to rozwiązać?
bo sam wykładnik dąży do 2
jak to rozwiązać?
 ?
?
 ?
wykładnik wg mnie dąży do 2 a nie do 4
?
wykładnik wg mnie dąży do 2 a nie do 4
 ?
?
