z tw. o 3 ciagach
Bartek:
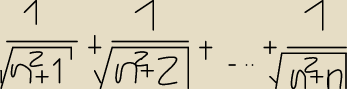
wzór na wyraz ogólny a
n=
a1+an2*n
i mam
30 mar 11:49
Bartek:
30 mar 11:54
Bartek: ta krecha jakis błąd mi wyskoczył bez tej krechy

30 mar 11:54
Bartek: niebardzo wiem jakie ciągi rozwazyć..
30 mar 11:59
Bartek: czy
mniejszy to bedzie 2* prawy pierwiastek
wiekszy 2 *lewy pierwiastek
bo wtedy było by że dążą do 1
?
30 mar 12:05
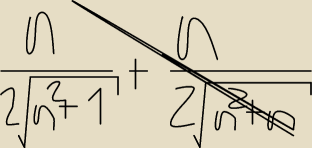
huehuehue: skad te 2 w mianowniku z postu 11:54 ? i moim zdaniem raczej tw. o 3 ciagach nie ma tu racji
| | n(n+1) | |
bytu musisz skorzystac z indukcji matematycznej ,np 1+2+3+...+n= |
| |
| | 2 | |
30 mar 12:07
Bartek: no wziąłem to ze wzoru na wyraz ogólny ciagu an=(a1+an)/2 *n
30 mar 12:09
Bartek: Tobie też 2 wmianownik wpadło

30 mar 12:09
Bartek: wzór na sumę jest to dokładnie
30 mar 12:10
Bartek: ma ktos pomysł jakiś?
30 mar 12:20
ICSP: to ja mam pytanie do ciebie :
co jest mniejsze :
30 mar 12:27
huehuehue: | n(n+1) | | 1 | |
| ≤ an ≤ |
| *(1+2+3+4+...n) |
| 2√n2+n | | √n2+n | |
30 mar 12:34
ICSP: chyba zadałem zbyt trudne pytanie

30 mar 12:42
Bartek: PRAWY JEST MNIEJSZY ICSP
30 mar 12:55
ICSP: no to teraz z lewej strony każdy zamienię na najmniejszy a z prawej każdy zamienię na
największy
i mam :
| n | | n | |
| ≤ an ≤ |
| |
| √n2 + n | | √n2 + 1 | |
prawa jak i lewa dążą do 1 to i środek musi dążyć do jedynki.
30 mar 12:57
Bartek: huehuehue troche nie wiem jak to zrobiłes tzn wiem co podostawiałeś ale dlaczego tak?
30 mar 12:57
ICSP: dlaczego tak ?
A jak myślisz co mi to dało że z każdej strony dostałem n identycznych wyrazów

30 mar 13:02
Bartek: na tak ale czy
n/(n2+1)1/2>niz an?
30 mar 13:06
Bartek: an masz w poście nr 2
30 mar 13:06
ICSP: To nie jest ciąg arytmetyczny


!
30 mar 13:07
Bartek: no ja juz nie kumam
an jest mniejszy niz pierwszy wyraz?
30 mar 13:17
Bartek: a większy niz ostatni?
30 mar 13:18
Bartek: w liczniku jest 1 a nie n
30 mar 13:19
ICSP: nie. Zauważ że an składa się z n wyrazów. Z lewej strony każdy z tych wyrazów ograniczyłem
przez najmniejszy. Po dodaniu n takich samych wyrazów dostaje w liczniku n. Identyczna
operacja z prawej strony tylko ograniczyłem przez największy
30 mar 13:43
Mila: W pierwszym wpisie napisałeś wzór na sumę n wyrazów ciągu arytmetycznego, a to nie jest suma
wyrazów c.a.
Rozpiszę Ci sposób
ICSP.
| | 1 | | 1 | | 1 | | 1 | |
an= |
| + |
| + |
| +.......+ |
| n wyrazów sumy |
| | √n2+1 | | √n2+2 | | √n2+3 | | √n2+n | |
| | 1 | | 1 | | 1 | | 1 | |
(1) |
| + |
| + |
| +.......+ |
| ≤ |
| | √n2+1 | | √n2+2 | | √n2+3 | | √n2+n | |
| 1 | | 1 | | 1 | | 1 | | n | |
| + |
| + |
| +.......+ |
| = |
| |
| √n2+1 | | √n2+1 | | √n2+1 | | √n2+1 | | √n2+1 | |
| | 1 | | 1 | | 1 | | 1 | |
(2) |
| + |
| + |
| +.......+ |
| ≥ |
| | √n2+1 | | √n2+2 | | √n2+3 | | √n2+n | |
| 1 | | 1 | | 1 | | 1 | | n | |
| + |
| + |
| +.......+ |
| = |
| |
| √n2+n | | √n2+n | | √n2+n | | √n2+1n | | √n2+n | |
| n | | 1 | | 1 | | 1 | | n | |
| ≤ |
| + |
| +.......+ |
| ≤ |
| |
| √n2+n | | √n2+1 | | √n2+2 | | √n2+n | | √n2+1 | |
| | n | | n | |
|
| →1 i |
| →1 stąd an→1 |
| | √n2+n | | √n2+1 | |
cnw
30 mar 16:50
Bartek: spoko teraz widzę , dzieki
30 mar 19:05
Mila: 
30 mar 20:58
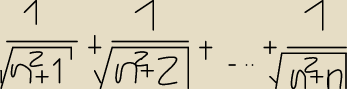 wzór na wyraz ogólny an=a1+an2*n
i mam
wzór na wyraz ogólny an=a1+an2*n
i mam







 !
!
