Monotoniczność funkcji. V.Abel: Witam, proszę o sprawdzenie/podpowiedź/wytknięcie błędów 1. Podaj wszystkie przykłady funkcji niemalejącej i nierosnącej jednocześnie. ad.1 Wg mnie tylko stała.

ciekawski: tak, to wszystko?

Mila: No i skąd wytrzasnąłeś ten problemik? Rozwiązuj zadania maturalne.

V.Abel: pytanie 2. dlaczego funkcja może przecinać asymptotę?

ciekawski: moze to nie jest najlepszy przyklad i ktos mnie poprawi, ale zwroc uwage na asymptotę spirali przy złotym podziale

ciekawski: http://upload.wikimedia.org/wikipedia/commons/e/ea/Asymptote02_vectorial.svg

Mila: No ta spirala to nie funkcja.

ciekawski: asymptota nie dotyczy tylko funkcji

Godzio: Dlaczego ? A dlaczego nie ?

	2x2 − 5x + 2
f(x) =
	3x2 − 10x + 3

	2		2
Asymptotą jest prosta y =		, ale f(0) =		. W definicji asymptoty nie ma nic o tym,
	3		3

że nie może przecinać wykresu funkcji

V.Abel: to dlaczego można ją przecinać ?

V.Abel: nie jest powiedziane, ze nie może, ale skoro intuicyjnie to wartość do której dąży funkcja i jej nie osiąga to nie za bardzo powinna ją przecinać

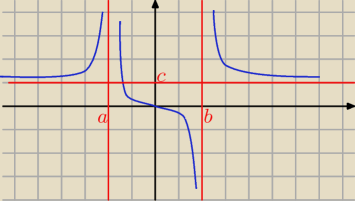
Basia: chodzi mniej więcej o takie funkcje asymptota y=c "działa" w przedziałach (−∞;a) i (b;+∞) "nie działa" w przedziale (a,b)

V.Abel: a jak jest np taka funkcja f(x)= x+0.9^x*sin9x to jak to wytłumaczyć?

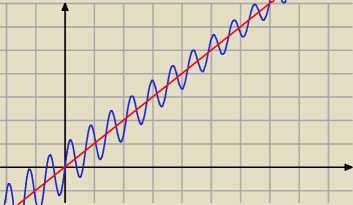
Basia: tu będzie asymptota ukośna przy x→+∞

f(x)		0,9x*sin9x
	= 1 +		→ 1
x		x

f(x) − x = 0,9^x*sin(9x) → 0 y = x f(kπ) = kπ+0,9^kπ*sin(9kπ) = kπ dla każdego x=kπ (ale nie tylko) wykres funkcji przetnie asymptotę te "brzuszki" są coraz niższe i "kręcą" się dokoła prostej y=x są coraz bliżej i bliżej, ale nigdy się nie "wyprostują" dlatego należy prostą y=x traktować jak asymptotę

V.Abel: Basia − czyli jak zdefiniować asymptotę? Jest to funkcja liniowa lub prosta do której funkcja "dąży", ale nie osiąga. Jak mamy do czynienia z asymptotą ukośną, to funkcja może ją przeciąć w zależności czy jest prawo− czy lewostronna. To chyba dobrze was zrozumiałem? Ale z tym ostatnim przykładem, to tak średnio. Jeżeli y=x jest asymptotą tej przecudnej funkcji, to widzę, że "brzuszki" starają się "prostować", ale się całkowicie nie "wyprostują", ok. Ale jak uzasadnić to, że dla tych kπ=x asymptotę się przecina? ? ? To w tym momencie już nie jest asymptota, bo funkcja dążyła do wartości i ją osiągnęła? . .

Mila: Podejdź kompleksowo do problemu i posłuchaj wykładu Pana doktora Janusza Górniaka. http://www.youtube.com/watch?v=PHFdo0u5Ay4

V.Abel: czyli funkcja może "oscylacyjnie", jak pan doktor powiedział zbliżać się do asymptoty− ok a czym są te punkty, które przecinają asymptotę, one są jakieś wyjątkowe?

V.Abel: ? ? ?