Wyznacz wszystkie wartości parametru m, dla których równanie sin2x+mcosx=0 martyna: Proszę o pomoc! Wyznacz wszystkie wartości parametru m, dla których równanie sin2x+mcosx=0 ma w przedziale <0,π> trzy rozwiązania. Prosze o dokładne wytłumaczeni co z czego się wzięło, bo w ogóle nie wiem od jakiej strony na to spojrzec. Nie wiem kiedy będą 3 rozwiązania, jak to sobie narysowac, czy sinus, czy cosinus..

martyna: Podbijam..

Basia: sin2x = 2sinx*cosx i stąd 2sinx*cosx + m*cosx = 0 cosx(2sinx + m) = 0 cosx = 0 ∨ 2sinx + m = 0 x = ^π₂ lub 2sinx = −m

	m
sinx = −
	2

	π
i to równanie ma mieć dwa rozwiązania różne od
	2

a to jest możliwe ⇔

	m
−		∊ (−1;1)
	2

	π
−1 i 1 odpadają bo sinx = 1 ⇔ x=		czyli byłoby tylko jedno rozwiązanie
	2

a wartości −1 sinus w przedziale <0;π> nie przyjmuje czyli też tylko jedno rozwiązanie czyli

	m
−1 < −		< 1 /*(−2)
	2

2 > m > −2

Mila: Wyznacz wszystkie wartości parametru m, dla których równanie sin2x+mcosx=0 ma w przedziale <0,π> trzy rozwiązania. sin2x+mcosx=0 ⇔ 2sinx *cosx+m cosx=0 cosx *(2sinx +m)=0

	π
cosx=0 i x∊ <0,π>⇔x=		masz jedno rozwiązanie, niezależnie od wartości m
	2

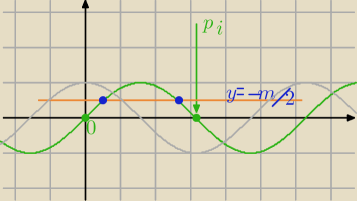
y=cos x lub

	−m
2sinx+m=0 ⇔2sinx=−m ⇔sinx=
	2

y=sinx w przedziale <0,π> ma wartości y∊<0,1> Chcemy mieć jeszcze 2 rozwiązania .

−m		−m
	≥0 i		<1
2		2