analityczna loro: W trójkącie równoramiennym ABC |AB|=|AC| dane są wierzchołki B=(1,−1), C=(4,0). Jedno z ramion trójkąta zawiera się w prostej x+2y−4=0. Na boku AB obrano taki punkt P że |AP|B| = 3:2. Znajdź równanie okręgu o środku P i stycznego do boku AC

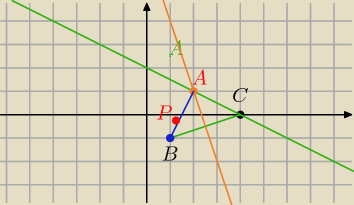
Mila: k: x+2y−4=0 2y=−x+4

	−1
k: y=		x+2
	2

|AB|=|AC|⇔BC jest podstawą. Wysokość opuszczona na podstawę zawiera się w symetralnej BC B=(1,−1), C=(4,0) Symetralna jest zbiorem punktów jednakowo odległych od końców odcinka: (x−1)²+(y+1)²=(x−4)²+y² stąd: s: y=−3x+7 Punkt A jest punktem przecięcia prostych k i s

	−1
y=−3x+7 i y=		x+2
	2

x=2 i y=1 A=(2,1) AB^→=[−1,−2]

	3		−3		−6
AP→=		[−1,−2]=[		,		]
	5		5		5

	−3		−6		3		6
A=(2,1)translacja o wektor [		,		]→P=(2−		,1−		)
	5		5		5		5

	2		−1
P=(1		,		)
	5		5

Równanie okręgu:

	7		1
(x−		)2+(y+		)2=r2
	5		5

Oblicz promień jako odległość P od prostej x+2y−4=0 dokończysz?